Az I. 465. feladat (2018. október)

I. 465. Adott egy $\displaystyle R$ sugarú kör alakú lap ($\displaystyle 10~\mathrm{mm} \le R \le 100~\mathrm{mm}$), amelyet leteszünk a földre. A lapra $\displaystyle N$ darab ($\displaystyle 1 \le N \le 100$) kisebb körlapot ejtünk véletlenszerűen úgy, hogy csak azokat az ejtéseket fogadjuk el, amelyeknél az ejtett lap nem lóg ki a földön lévő lapról. Az ejtett lapok átfedhetik egymást, de teljes egészében a lefektetett nagyobb lapon vannak. Kérdés, hogy a nagy lap területének hány százaléka nincs az $\displaystyle N$ darab kisebb körlappal lefedve. Készítsünk szimulációs programot, amely modellezi a jelenséget, és minél pontosabban válaszol a kérdésre.

A program a standard bemenet első sorából olvassa be $\displaystyle R$ és $\displaystyle N$ értékét (egészek), valamint a következő sorból a leejtett körlapok sugarát (mindegyik sugár 1 mm-nél nagyobb, de $\displaystyle R$-nél kisebb egész érték). A standard kimenetre írjuk ki a lefektetett körlap nem lefedett részének területét négyzetmilliméter pontossággal.

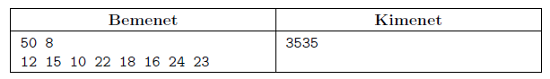
Beküldendő egy i465.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2018. november 12-én LEJÁRT.

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Békési Péter, Horcsin Bálint, Nagy 793 Márton, Ürmössy Dorottya, Zámborszky Balázs.
8 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.

A KöMaL 2018. októberi informatika feladatai