Az I. 475. feladat (2019. február)

I. 475. Egy \(\displaystyle N\) oldalhosszúságú szabályos háromszög két fajta színű, egységnyi oldalú szabályos háromszögekből áll. Vizsgáljuk az \(\displaystyle N\) oldalhosszúságú háromszögben kirajzolódó egyszínű, szabályos háromszögeket. Készítsünk programot i475 néven, amely megadja mindkét színhez a lehető legnagyobb területű szabályos háromszög oldalának hosszát.

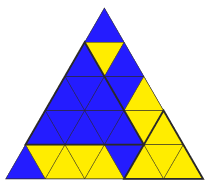
A program olvassa be a standard bemenet első sorából az \(\displaystyle N\) oldalhosszúságot (\(\displaystyle 1\le N\le 100\)), majd a következő \(\displaystyle N\) sorból a háromszög adott szintjén lévő egységnyi háromszögek színének kezdőbetűjét (\(\displaystyle \texttt{k}=\text{kék}\), \(\displaystyle \texttt{s}=\text{sárga}\)).

A program a standard kimenetre írja ki a kék, majd a következő sorba a sárga háromszögekből álló legnagyobb egyszínű, szabályos háromszög oldalhosszúságát.

Példa:

Beküldendő egy tömörített i475.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2019. március 11-én LEJÁRT.

Mintamegoldásként Horcsin Bálint budapesti, 10. évfolyamos diák munkáját adjuk közre:

i475.cpp

Tesztállományok: tesztharomszog.zip

Az 5. bemenet ábrája:

Statisztika:

5 dolgozat érkezett.
10 pontot kapott:	Horcsin Bálint.
8 pontot kapott:	2 versenyző.
7 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2019. februári informatika feladatai