Az I. 538. feladat (2021. május)

I. 538. A puzzle játék során lapokat kell ábrarészlet, illetve az oldalak illeszkedése alapján összerakni. Készítsünk programot i538 néven, amely egy \(\displaystyle N\times N\)-es puzzlet kirak az összekevert lapokból. A puzzle biztosan kirakható, a lapok mind rendelkezésre állnak és nem kell őket forgatni. A lapok 1-től \(\displaystyle N\times N\)-ig számozottak, és az oldalakat, ezzel az illeszkedést a szomszéd lapokhoz nem ismétlődő pozitív egész számok adják. Ha a lap egyik oldalán 0 érték szerepel, akkor az a puzzle szélén helyezkedik el.

A program standard bemenetének első sorában \(\displaystyle N\) (\(\displaystyle N\le 10\)), a sorok és oszlopok száma van. A következő \(\displaystyle N^2\) sorban, soronként 5 darab nemnegatív szám szerepel. Az első a lap sorszáma, a mintán a 3-as, majd felülről indulva az óramutató járásának megfelelően az oldalakat azonosító számok. Azokat a lapokat lehet összerakni, ahol az illesztendő oldalakon azonos szám szerepel.

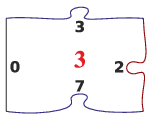
A program standard kimenetén szóközzel elválasztva a kirakott puzzle kártyáinak sorszáma szerepeljen sorfolytonosan.

Magyarázatul a kirakott puzzle:

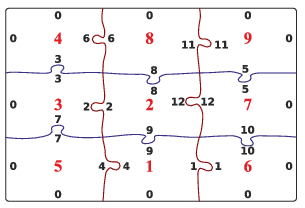
Beküldendő egy tömörített i538.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2021. június 15-én LEJÁRT.

Mintamegoldás:

A mintamegoldás Borbély-Bartis Gergely, a pécsi Ciszterci Rend Nagy Lajos Gimnázium 9. osztályos tanulójától származik: i538.py

darabok.txt

Statisztika:

10 dolgozat érkezett.
10 pontot kapott:	Bagladi Milán Zsolt, Borbély-Bartis Gergely, Gyönki Dominik, Horcsin Bálint, Mályusz Etre Magnusz, Nagy 292 Korina, Tóth 057 Bálint, Ürmössy Dorottya, Vadász Levente Márton.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2021. májusi informatika feladatai