 |
Az I. 575. feladat (2022. november) |
I. 575. Egy kiszámolóban tíz ember áll körben, és a következő szabályok szerint játszanak:
- 1. Először mindenki gondol egy négyjegyű egész számra. Ezután a játék menetekből áll addig, amíg valakinek 0 nem lesz a száma. Ekkor ő a kiszámoló nyertese.
2. Az első menet előtt véletlenszerűen kisorsolnak egy játékost a 10-ből, ő lesz az első menetben a ,,számoló''.
3. A ,,számoló'' megnézi a számának utolsó számjegyét (legyen ez k), és számol saját magától indulva k lépést a körben előre, így kiszámolja a következő körben ,,számoló'' játékost. Ha k értéke 0, akkor ismét ő lesz a számoló. Ezután elhagyja a saját számának utolsó jegyét, és az így kapott szám az ő száma.
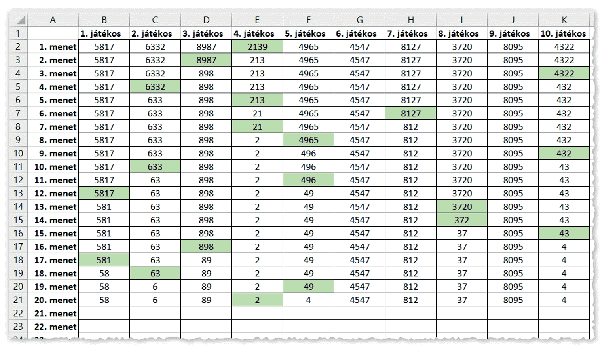
4. A játék minden menetében a 3. pontban leírtak szerint jár el a számláló, kivéve akkor, ha az ő száma már egyjegyű. Ebben az esetben a játék véget ér, ő a nyertes.
Szimuláljuk a játékot táblázatkezelő segítségével az alábbi mintát felhasználva. Minden sorban számítsuk ki az egyes játékosok számát, illetve jelezzük feltételes formázással, hogy ki a számoló játékos. A táblázatban csak az utolsó menetig jelenjenek meg adatok, de a munkafüzet legyen felkészítve a lehető leghosszabb, azaz legtöbb menetből álló játékra is.
A megoldást a táblázatkezelő beépített függvényeivel készítsünk el, az L oszloptól jobbra segédcellákat használhatunk, de saját függvényt vagy makrót ne alkalmazzunk. A táblázat formázását a mintához hasonlóan alakítsuk ki.
Beküldendő egy tömörített i575.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.
(10 pont)
A beküldési határidő 2022. december 15-én LEJÁRT.
Mintamegoldásként Gyönki Dominik egri, 10. évfolyamos versenyző megoldását (i575gyd.xlsx) és Nagy Korina kecskeméti, 10. évfolyamos tanuló munkáját (i575nk.xlsx) adjuk közre.
Statisztika:
12 dolgozat érkezett. 10 pontot kapott: Gyönki Dominik, Hinek Milán, Horváth Milán, Kövesi Alíz, Nagy 292 Korina, Vadász Levente Márton. 9 pontot kapott: Szabó Imre Bence. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2022. novemberi informatika feladatai
|
|

