Az I. 584. feladat (2023. február)

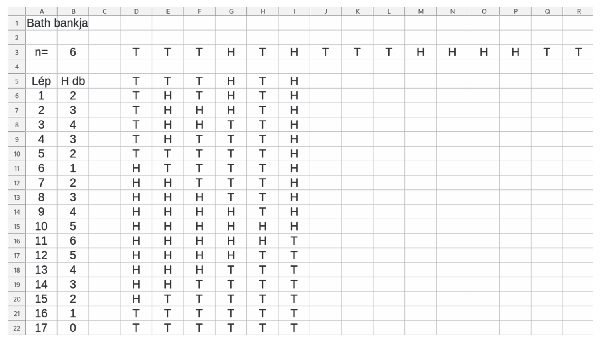
I. 584. (É). A 60. Nemzetközi Matematikai Diákolimpia 5. feladatában szerepel a következő: ,,Bath Bankja érméket bocsát ki, melyeknek egyik oldalán $\displaystyle \mathrm{H}$, másik oldalán $\displaystyle \mathrm{T}$ betű látható. Harrynek $\displaystyle n$ ilyen érméje van, amelyek előtte balról jobbra, egy sorban vannak elrendezve. Harry ismételten végrehajtja a következő műveletet: ha pontosan $\displaystyle k>0$ olyan érme van, amin $\displaystyle \mathrm{H}$ van felül, akkor megfordítja a balról $\displaystyle k$-adik érmét; máskülönben minden érmén $\displaystyle \mathrm{T}$ van felül, és ekkor Harry megáll. Például $\displaystyle n=3$ esetén a $\displaystyle \mathrm{THT}$ sorozatból indulva $\displaystyle \mathrm{THT} \to \mathrm{HHT} \to \mathrm{HTT} \to \mathrm{TTT}$ a lépések sorozata, ami három lépés után megáll.''

Modellezzük a feladatban leírt $\displaystyle n$ ($\displaystyle n\le 30$) hosszú sorozat viselkedését legfeljebb 100 lépésen keresztül táblázatkezelő segítségével!

1. Hozzunk létre egy táblázatkezelő munkafüzetet és mentsük bathbankja néven a program alapértelmezett formátumában.

2. Helyezzük el egy munkalapon a ,,Bath bankja'' szöveget az A1-es cellába, valamint az ,,n='' szöveget az A3-as cellába.

3. Hozzunk létre a D3-as cellában és a sorban tőle jobbra egy ,,T'' és ,,H'' betűkből álló 30-tagú sorozatot véletlenszám felhasználásával úgy, hogy a két betűt egyenlő eséllyel kapjuk minden cellában.

4. Írjunk be egy pozitív egész számot a B3-as cellába, amely megadja a vizsgált sorozat hosszát. A 3. sorban generált sorozatból, illetve a később létrehozott sorozatokból csak az első $\displaystyle n$ darab betűvel foglalkozunk a szimulációban.

5. Adjuk meg képlettel, hogy a generált számokból az első $\displaystyle n$ darab az 5. sor megfelelő celláiban is megjelenjen, míg a sor további cellái üresen jelenjenek meg.

6. Adjunk meg a B6:B105 tartomány celláiban olyan képletet, amely megadja az adott cella feletti sorban a D oszlopban és attól jobbra lévő betűsorozatban a ,,H'' betűk számát.

7. Adjunk meg a D6:M105 tartomány celláiban olyan képletet, amely a feladat leírásának megfelelően a sorozat $\displaystyle k$-adik betűjét kicseréli, míg a többi betűt átveszi a felette lévő sorozatból, ahol $\displaystyle k$ az előző sorban lévő ,,H'' betűk száma.

8. Állítsunk be a munkalap minden cellájára a mintához hasonló, a tartalom megjelenítéséhez megfelelő oszlopszélességet és formázzuk a munkalapot a mintának megfelelően.

Beküldendő egy tömörített i584.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.

(10 pont)

A beküldési határidő 2023. március 16-án LEJÁRT.

Mintamegoldásként Hinek Milán szolnoki versenyző táblázatát (bathbankja.xlsx) és Gyönki Dominik egri tanuló megoldását (bathbankja.xlsx) adjuk közre.

Statisztika:

5 dolgozat érkezett.
10 pontot kapott:	Badics Balázs, Gyönki Dominik, Hinek Milán, Horváth Milán, Szabó Imre Bence.

A KöMaL 2023. februári informatika feladatai