Az I. 596. feladat (2023. szeptember)

I. 596. A számok tulajdonságaik alapján különféle érdekes neveket kaptak. Vannak például páratlan számok, háromszögszámok, prímszámok, tökéletes számok stb. Az egyik ilyen különleges számfajtát a boldog számok alkotják. Ők azok a pozitív egészek, amelyekre az alábbi műveletsorozatot végrehajtva a végeredményként kapott szám 1 lesz: a szám számjegyeinek négyzetösszegét képezzük, majd az így kapott szám számjegyeinek négyzetösszegét képezzük és így tovább. A képzést egészen addig folytatjuk, amíg egyjegyű számot nem kapunk.

Nézzük például az 527-et: a számjegyek négyzetösszege \(\displaystyle 25+4+49=78\). A 78 számjegyeinek négyzetösszege \(\displaystyle 49+64=113\). A 113 számjegyeinek négyzetösszege \(\displaystyle 1+1+9=11\), majd a 11 számjegyeinek négyzetösszege 2. Ez az első egyjegyű szám a sorozatban. Mivel ez a szám nem 1-es, így az 527 nem boldog szám.

Készítsünk programot i596 néven, amely bekér egy pozitív egész számot, majd azzal elvégzi a műveletsorozatot, végül megadja, hogy a szám boldog szám-e. A program a műveletsorozat minden részeredményét és eredményét jelenítse meg az alábbi mintának megfelelően:

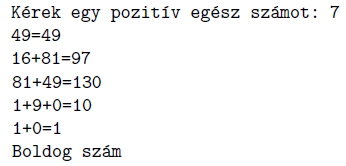
vagy

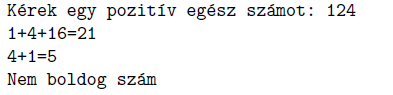
Beküldendő egy tömörített i596.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2023. október 16-án LEJÁRT.

Mintamegoldásként Kissik Márton esztergomi, 10. évfolyamos tanuló Python nyelven készült munkáját (i596.py), Pál Benedek József szegedi, 12. évfolyamos versenyző C++ nyelven készült programját (i596.cpp) munkáját adjuk közre.

Statisztika:

42 dolgozat érkezett.
10 pontot kapott:	Anastasiia Nosyk, Bátorfi Balázs, Bodányi Zsigmond Balázs, Bucsai Máté, Bukta Balázs, Csíkos 256 Benjamin, Daruka Balázs, Dömők Bernadett, Farkas Bence Sándor, Gincsai Gábor, Gyönki Dominik, Halmosi Dávid, Hegyi Benedek, Illés Gergely Levente, Kádas Dániel, Kiss Ákos, Kissik Márton, Lukács Gergely, Lukacs Milán Levente , Nagy 292 Korina, Nagy Borbála Adrienn, Oláh Barnabás, Pál Benedek József , Puppi Barna, Rózsa Zsombor, Sánta Gergely Péter, Schmidt Marcell, Simon-Hajdú Gergő, Sógor-Jász Soma, Szabó Imre Bence, Szász Dávid, Szörényi Zalán András , Varga462 Vilmos, Viszkocsil Norton.
9 pontot kapott:	Debreczeni Huba, Pavlisinec Balázs Máté.
8 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2023. szeptemberi informatika feladatai