 |
Az I. 608. feladat (2023. december) |
I. 608. Egy vasútvonal állomásain a szabadban tárolják a betakarított cukorrépát. A cukorgyári kampány előtt az egyik állomásra fedett tárolót szeretnének építeni és a termést odaszállítani a többi állomásról, hogy a répa minőségromlása minél kisebb legyen. Melyik állomásra tervezzék a fedett tárolót, ha a költség a szállítási út hosszával és a szállított tömeggel is egyenesen arányos?
Készítsünk programot i608 néven, amely a megadja az N állomás előző állomástól mért H[N] távolságának és az ott tárolt cukorrépa T[N] tömegének ismeretében, hogy melyik állomáson legyen a fedett tároló a minimális szállítási költség mellett.
A program standard bemenetének első sorában a vasútállomások (1≤N≤100) száma található. A következő N sorban a vasútállomások (1≤H[i]≤50) kilométerben mért távolsága szerepel az előző állomástól, és az ott tárolt (1≤T[i]≤1000) cukorrépa tömege van tonnában megadva. Az első állomásnál 0 távolság szerepel.
A program a standard kimenetre írja ki, hogy hányadik vasútállomásra érdemes tervezni a fedett tárolót és mennyi az ideszállítás költsége. Több azonos költségű megoldás esetén a kisebb sorszámú vasútállomást adjuk meg.
Példa:
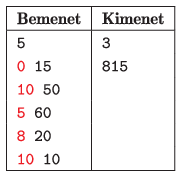
Magyarázat: 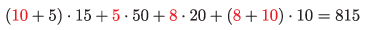
Beküldendő egy tömörített i608.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2024. január 15-én LEJÁRT.
Néhány a teszteléshez használt állomány: be1.txt, be2.txt, be3.txt, be4.txt, be5.txt
és a kimenetek: ki1.txt, ki2.txt, ki3.txt, ki4.txt, ki5.txt
Minta megoldás:
Pál Benedek József a szegedi Radnóti Miklós Kísérleti Gimnázium 12. osztályos tanulójának munkája: main.cpp
Statisztika:
16 dolgozat érkezett. 10 pontot kapott: Anastasiia Nosyk, Bátorfi Balázs, Gyönki Dominik, Hajós-Szabó Máté, Halmosi Dávid, Nagy 292 Korina, Pál Benedek József , Puppi Barna, Schmidt Marcell, Simon-Hajdú Gergő, Sógor-Jász Soma, Szabó Imre Bence. 2 pontot kapott: 2 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2023. decemberi informatika feladatai
|
|

