 |
Az I. 618. feladat (2024. február) |
I. 618. Középosztósnak nevezik azokat a legalább háromjegyű számokat, ahol a szám első és utolsó jegyét elhagyva a kapott szám osztható az első és utolsó jegy összegével. Duplaközéposztósnak nevezik azokat a legalább ötjegyű középosztós számokat, ahol a szám első és utolsó jegyét elhagyva a kapott szám szintén középosztós.
Például \(\displaystyle 2124\) középosztós, mert a közepén lévő szám, ami \(\displaystyle 12\), osztható \(\displaystyle {(2+4=)6}\)-tal. A \(\displaystyle 321243\) dupla középosztós, mert \(\displaystyle 2124\) középosztós, és osztható \(\displaystyle {(3+3=)6}\)-tal. A leírásból következik, hogy a duplaközéposztós számok legalább ötjegyűek.
Állítsuk elő táblázatkezelő segítségével az összes legfeljebb hatjegyű duplaközéposztós számot, és válaszoljunk néhány ezekkel kapcsolatos kérdésre!
- Nyissunk meg egy üres munkafüzetet, generáljuk a kívánt számokat a munkalap A oszlopába. Mentsük el a munkafüzetet gener néven.
- Nyissuk meg a kozep.xlsx munkafüzetet és másoljuk át a generált számokat ebbe a munkafüzetbe függőlegesen az A3-as cellától kezdve. Az első szám az A3-as cellában legyen, a számok között ne legyen üres cella.
- Válaszoljunk az I3:I9 tartomány celláiban függvény segítségével a tőlük balra feltett kérdésekre.
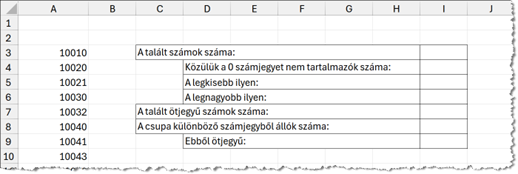
Magyarázatként nézzük a \(\displaystyle 10\,032\) számot: a szélei \(\displaystyle 1\) és \(\displaystyle 2\), ezek összege \(\displaystyle 3\). A szám közepe \(\displaystyle 003\), ami valójában \(\displaystyle 3\); \(\displaystyle 3\) osztható \(\displaystyle 3\)-mal. A középső \(\displaystyle 003\) szélei \(\displaystyle 0\) és \(\displaystyle 3\), összegük \(\displaystyle 3\). A szám közepe \(\displaystyle 0\), és \(\displaystyle 0\) is osztható \(\displaystyle 3\)-mal. Vagy például a \(\displaystyle 797\,562\) szám szélső jegyei \(\displaystyle 7\) és \(\displaystyle 2\), összegük \(\displaystyle 9\), és a közepe, \(\displaystyle 9756\) osztható \(\displaystyle 9\)-cel, a \(\displaystyle 9756\) szélei \(\displaystyle 9\) és \(\displaystyle 6\), összegük \(\displaystyle 15\), és a közepe \(\displaystyle 75\) osztható \(\displaystyle 15\)-tel.
Segédszámításokat a gener munkafüzetben a B oszloptól jobbra, a kozep munkafüzetben a J oszloptól jobbra végezhetünk. A megoldásban saját függvény vagy makró nem használható.
Beküldendő egy tömörített i618.zip állományban a gener és a kozep táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a generáláskor alkalmazott módszer, a táblázatkezelő neve, verziószáma.
Letölthető fájl: kozep.xlsx.
(10 pont)
A beküldési határidő 2024. március 18-án LEJÁRT.
Gyönki Dominik mintaszerű megoldása. I618.ZIP
Statisztika:
8 dolgozat érkezett. 10 pontot kapott: Gyönki Dominik, Nagy 292 Korina. 7 pontot kapott: 3 versenyző. 6 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2024. februári informatika feladatai