Az I. 641. feladat (2024. november)

I. 641. A feladat a szeptemberi számban megjelent I. 633. feladat folytatása.

Most háromféle speciális prímet keresünk az első százezer prímszám között, ezek a palindromprímek, a mírpszámok és a Bölcsföldi-Birkás prímek. Nézzük is ezek definícióit:

Palindromprímnek nevezzük azt a $\displaystyle p$ prímszámot, amelynek $\displaystyle 10$-es számrendszerbeli alakja palindrom, vagyis balról és jobbról olvasva ugyanaz a szám. Például: a $\displaystyle 12421$ ilyen prím.

Mírpszámnak azt a prímet nevezzük, amelynek $\displaystyle 10$-es számrendszerbeli alakja visszafelé (jobbról balra) olvasva is prím, de a szám nem palindromprím. Például: az $\displaystyle 1009$ ilyen szám, hiszen nem palindrom, de a $\displaystyle 9001$ is prím.

Bölcsföldi-Birkás prímnek azt a prímet nevezzük, amelynél az egyes számjegyek, a számjegyek száma és azok összege is prím. Például: a $\displaystyle 757$ ilyen szám, hiszen számjegyei ($\displaystyle 5$ és $\displaystyle 7$) prímek, a számjegyek száma ($\displaystyle 3$) is prím és a számjegyek összege ($\displaystyle 19$) is prím.

1. Egy üres táblázatkezelő munkafüzetben nevezzük át „prím100000''-re a munkalapot, a munkafüzetet mentsük prim_2-resz néven.
2. Illesszük be az A3 cellától az első $\displaystyle 100\,000$ prím listáját a 100000prim.txt fájlból. Az első két sorba oszlopfeliratok kerülhetnek a számításokhoz.
3. Válogassuk ki a három prímcsoport első $\displaystyle 100\,000$ prím közé eső tagjait. A számításokat ezen a munkalapon végezzük.
4. Hozzunk létre egy spec nevű munkalapot, amelynek A, B és C oszlopaiban szerepeljen az első sorban a prímcsoportok neve, majd alattuk növekvő sorrendben helykihagyás nélkül az adott csoportok prímszámai.
5. Ezek után végezzünk statisztikai vizsgálatokat, amelyekben a legfeljebb hatjegyű prímeket vizsgáljuk, mert nincs a listában az összes hétjegyű prímszám.
1. Határozzuk meg, hogy a pontosan egy-, kettő-, $\displaystyle \ldots$, hatjegyű természetes számok hány százaléka prím. Készüljön erről oszlopdiagram külön diagramlapra, amelynek neve legyen százalék.
2. Határozzuk meg, hogy a prímekben hányszor fordulnak elő az egyes számjegyek, például a $\displaystyle 89393$ számban van két hármas, egy nyolcas és két kilences számjegy. Készüljön erről oszlopdiagram külön diagramlapra a minta szerint, melynek neve legyen számjegyek.
3. Jelenítsük meg az A100004-es cellában az alábbi szöveget: „táv > 99'' és a B100004-es cellában adjuk meg, hogy hány esetben fordul elő, hogy két egymást követő prímszám különbsége legalább $\displaystyle 100$.
4. Jelenítsük meg az A100005-ös cellában az alábbi szöveget: „maxtáv'' és a B100004 es cellában az első $\displaystyle 100\,000$ prím esetén a szomszédos prímszámok maximális különbségének értékét, a C100004 és D10004 cellákban pedig a két szóban forgó prímszámot.

A 6., 7. és 8. pont módosításaival elérhető, hogy 5 MB alá kerüljön a fájlméret, és feltölthető legyen a megoldás.

1. A prim100000 munkalapon cseréljük le oszloponként az első tizenhét sor utáni képleteket az értékükre. Hasonlóan járjunk el a 100002 sor alatti adatokkal és a két diagram adataival, továbbá a teljes spec munkalappal. Ezzel is csökkentjük a fájl méretét.
2. Töröljük a prim100000 munkalap 20000:80000 sorának tartalmát.
3. Végül a munkafüzetet mentsük az eredeti nevén xlsb formátumban (bináris munkafüzetként).

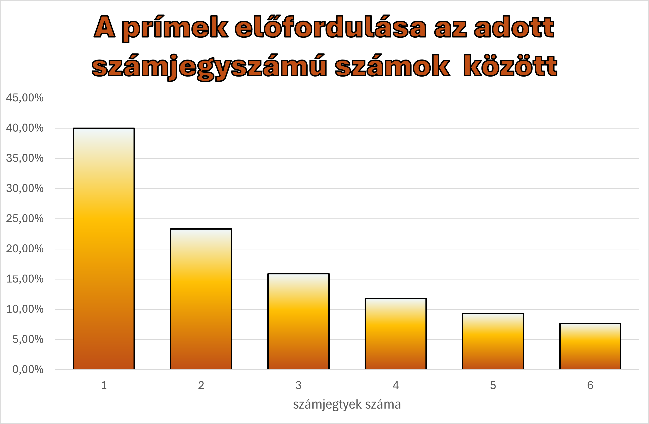
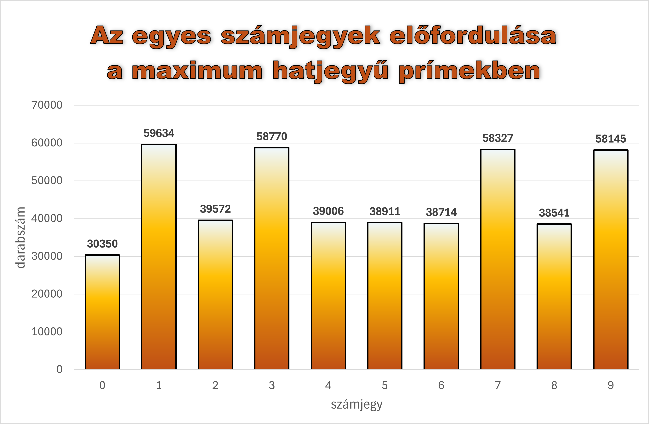
Segédszámításokat a prím100000 munkalapon a B, a spec munkalapon pedig a D oszloptól jobbra lehet végezni. A megoldásban saját függvény vagy makró nem használható.

Beküldendő az i641.zip tömörtett állomány a munkafüzettel és egy rövid dokumentációval, amelyben szerepel a kiválogatások magyarázata, a táblázatkezelő neve, verziószáma.

Letölthető fájl: 100000prim.txt

(10 pont)

A beküldési határidő 2024. december 16-án LEJÁRT.

Bencze Mátyás kiemelkedő megoldása prim2-resz.xlsb

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Bencze Mátyás, Gyönki Dominik, Illés Gergely Levente, Szabó Imre Bence.
8 pontot kapott:	3 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. novemberi informatika feladatai