A K/C. 753. feladat (2023. január)

K/C. 753. Az $\displaystyle A$ csúcsú szög egyik szárán lévő $\displaystyle B$, $\displaystyle C$, $\displaystyle D$ és $\displaystyle E$ pontokra, illetve a másik szárán lévő $\displaystyle F$, $\displaystyle G$, $\displaystyle H$ és $\displaystyle I$ pontokra igaz, hogy $\displaystyle AB=BG=GD=DI=IE=EH=HC=CF=FA$. Mutassuk meg, hogy a $\displaystyle CEH$ és az $\displaystyle IGD$ háromszögek szabályosak.

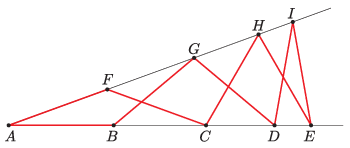
(5 pont)

A beküldési határidő 2023. február 10-én LEJÁRT.

Megoldás. Jelöljük az $\displaystyle A$ csúcsnál levő szöget $\displaystyle \alpha$-val. Az $\displaystyle ACF$ egyenlő szárú háromszög $\displaystyle C$-nél levő belső szöge is $\displaystyle \alpha$, ezért $\displaystyle AFC\sphericalangle=180^{\circ}-2\alpha$.

A $\displaystyle HFC\sphericalangle=2\alpha$, mivel ez a szög az $\displaystyle ACF$ háromszög külső szöge, és így az $\displaystyle FHC$ egyenlő szárú háromszögben $\displaystyle FHC\sphericalangle=2\alpha$, illetve

$\displaystyle FCH\sphericalangle=180^{\circ}-4\alpha.$

$\displaystyle ECH\sphericalangle=3\alpha$, mert ez a szög az $\displaystyle ACH$ háromszög külső szöge. Innen azonnal következik, hogy a $\displaystyle CEH$ egyenlő szárú háromszögben $\displaystyle CEH\sphericalangle=3\alpha$ és $\displaystyle EHC\sphericalangle=180^{\circ}-6\alpha$.

Ebből és $\displaystyle FHC\sphericalangle=2\alpha$-ból következően az $\displaystyle IHE$ egyenlő szárú háromszögben

$\displaystyle IHE\sphericalangle=HIE\sphericalangle=4\alpha.$

A $\displaystyle BDG$ egyenlő szárú háromszögben $\displaystyle DBG\sphericalangle=2\alpha$, mert ez a szög az $\displaystyle AGB$ egyenlő szárú háromszög külső szöge, ezért $\displaystyle BDG\sphericalangle=2\alpha$ és $\displaystyle DGB\sphericalangle=180^{\circ}-4\alpha$ is teljesül.

Az $\displaystyle AGB$ egyenlő szárú háromszögben $\displaystyle BGA\sphericalangle=\alpha$, tehát $\displaystyle DGB\sphericalangle+BGA\sphericalangle=180^{\circ}-3\alpha$, de akkor $\displaystyle DGI\sphericalangle=3\alpha$, ennek következményeként pedig a $\displaystyle IGD$ egyenlő szárú háromszögben $\displaystyle DIG\sphericalangle=3\alpha$ is igaz.

Mivel előbb már beláttuk, hogy $\displaystyle HIE\sphericalangle=4\alpha$, ezért előző eredményünkből

$\displaystyle DIE\sphericalangle=\alpha$

következik. Ebből adódik a $\displaystyle DEI$ háromszögben, hogy $\displaystyle EDI\sphericalangle=4\alpha$, hiszen ez a szög $\displaystyle ADI$ háromszög külső szöge.

A $\displaystyle DEI$ egyenlő szárú háromszög, ez azt jelenti, hogy

$\displaystyle DEI\sphericalangle=4\alpha$

is igaz. A $\displaystyle DEI$ háromszög szögeinek összege tehát $\displaystyle 4\alpha+4\alpha+\alpha=9\alpha=180^{\circ}$, ahonnan

$\displaystyle \alpha=20^{\circ}.$

A $\displaystyle CEH$ egyenlő szárú háromszögben tehát $\displaystyle CEH\sphericalangle=ECH\sphericalangle=3\alpha=60^{\circ}$, és így a háromszög $\displaystyle H$ csúcshoz tartozó belső szöge is $\displaystyle 60^{\circ}$-os, vagyis a háromszög valóban szabályos.

Az $\displaystyle IGD$ egyenlő szárú háromszögben pedig $\displaystyle DIG\sphericalangle=DGI\sphericalangle=3\alpha=60^{\circ}$, eszerint ebben a háromszögben a $\displaystyle D$ csúcsnál $\displaystyle 60^{\circ}$-os belső szög van, ezért ez is szabályos háromszög.

Megjegyzés.

Könnyen bizonyítható, hogy az ábra az $\displaystyle IAE\sphericalangle=\alpha$ szög szögfelezőjére szimmetrikus.

Statisztika:

160 dolgozat érkezett.
5 pontot kapott:	105 versenyző.
4 pontot kapott:	17 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	9 versenyző.
Nem versenyszerű:	10 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2023. januári matematika feladatai