A K/C. 757. feladat (2023. február)

K/C. 757. Kati egy $\displaystyle 4\times4$-es négyzetrácsos papírlapot szeretne a rácsvonalak mentén kisebb darabokra vágni ollóval. Mutassuk meg, hogy pontosan 11-féle puzzle-t tudna kivágni úgy, hogy a kivágásnak megfelelően kirakott puzzle az eredeti $\displaystyle 4\times4$-es négyzet mind a négy szimmetriatengelyére szimmetrikus lesz. Ez például egy megfelelő puzzle:

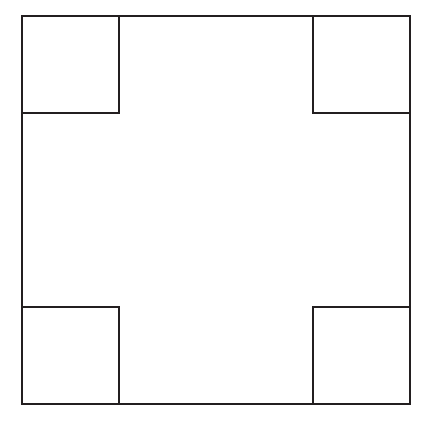
(5 pont)

A beküldési határidő 2023. március 10-én LEJÁRT.

Megoldás. A szimmetriák miatt bizonyos szakaszokat egyszerre húzhatunk csak be, ha a puzzle vonalainak tervrajzát készítjük. Négy ilyen szakasz-csoport van ($\displaystyle a$, $\displaystyle b$, $\displaystyle c$ és $\displaystyle d$).

Ezek berajzolásának kombinációiból állnak össze a felbontások. Mivel minden egyes szakaszcsoport vagy be van rajzolva, vagy nincs, ezért $\displaystyle 2^4=16$-féle tervrajz lehet maximum, ám nem mindegyik szakasz-csoport választáshoz tartozik valódi vágás-tervrajz, mert előfordul, hogy nem négyzetlapokból álló alakzatokat kapunk.

Ilyen választások a $\displaystyle b$ (önmagában), a $\displaystyle c$ (önmagában), az $\displaystyle a$ és $\displaystyle b$ egyesítése, és az $\displaystyle a$ és $\displaystyle c$ egyesítése. Így a 16 lehetőség közül 4 nem megfelelő, tehát 12 igen. Ezek meg is valósulhatnak:

Viszont az elsőben nincs szükség vágásra, tehát 11-féle puzzle-t tudna kivágni a feltételeknek megfelelően.

Statisztika:

128 dolgozat érkezett.
5 pontot kapott:	Aaishipragya Kahaly, Barna Márton, Becsei Attila, Bettesch Emma Léda, Domján István, Egyházi Godó, Feczkó Illés Tivadar, Gál András, Hauser Márton, Hodossy Réka, Illés Dóra, Iván Máté Domonkos, Jeviczki Ádám, Juhász Noel, Jurácsik Marcell, Kendrovszki Dominik, Kerekes András, Klement Tamás, Kószó Ferenc, Kovács Artúr Mihály, Kovács Barnabás, Kovács Dániel, Krüpl Boglárka, Lestár Sarolta, Márfai Dóra, Masa Barnabás, Mező Levente, Nagy 707 Botond, Németh Hanna Júlia , Pletikoszity Martin, Ráthonyi Levente Marcell, Somogyi Dóra, Sukola Bence, Sütő Áron, Szabó Donát, Tajta Sára, Teveli Jakab, Tóth 207 Bence, Tömböly 299 Áron, Török Eszter Júlia, Ujpál Bálint, Varga 511 Vivien, Virág Máté Gergely, Wodala Gréta Klára, Zaránd Kristóf.
4 pontot kapott:	47 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	6 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2023. februári matematika feladatai