A K/C. 758. feladat (2023. február)

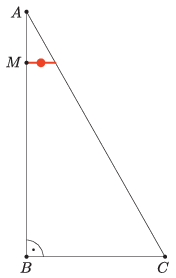
K/C. 758. Egy derékszögű háromszög alakú vitorlán a hajóosztály piros jele olyan magasságban van felfestve, hogy $\displaystyle MA + AC = CB + BM$. Ha $\displaystyle BM = 7$ m és $\displaystyle CB = 5$ m, akkor mennyivel van magasabban a vitorla felső csúcsa a jeltől?

(5 pont)

A beküldési határidő 2023. március 10-én LEJÁRT.

Megoldás. Az $\displaystyle ABC$ derékszögű háromszögre felírva a Pitagorasz-tételt: $\displaystyle AB^2 + CB^2 = AC^2$, azaz $\displaystyle (MA + 7)^2 + 5^2 = AC^2$, ugyanakkor $\displaystyle AC^2 = (CB + BM) - MA = 12 - MA$, amit az első egyenletbe helyettesítve:

$\displaystyle (MA + 7)^2 + 5^2 = (12 – MA)^2.$

Ebből $\displaystyle MA^2 + 14MA + 49 + 25 = 144 - 24MA + MA^2$, egyszerűsítve $\displaystyle 14MA + 74 = 144 - 24MA$, ahonnan $\displaystyle 38MA = 70$, azaz $\displaystyle MA \approx 1,84$ m távolságra van a vitorla felső csúcsától a jelzés.

Statisztika:

208 dolgozat érkezett.
5 pontot kapott:	168 versenyző.
4 pontot kapott:	15 versenyző.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	10 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	5 dolgozat.

A KöMaL 2023. februári matematika feladatai