A K/C. 762. feladat (2023. március)

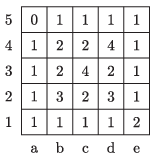
K/C. 762. Egy \(\displaystyle 5\times5\)-ös táblázat huszonöt mezőjét valamilyen sorrendben kiválasztjuk, és egy számot írunk rá. Az aktuálisan választott mezőre azt a számot írjuk, amely megmutatja, hogy annak a mezőnek addig hány olyan oldalszomszédja van már, amelyre írtunk számot.

(Ezt a táblázatot pl. az alábbi sorrendben tölthettük ki: a5, b5, c5, d5, e5, e4, e3, e2, a4, a3, a2, a1, b1, c1, d1, e1, \(\displaystyle \ldots\,\).)

Készítsünk még két ilyen kitöltést. Adjuk össze a kitöltésben lévő számokat.

Bizonyítsuk be, hogy akárhogyan töltjük ki a szabálynak megfelelően a táblázatot, a számok összege minden esetben 40 lesz.

(5 pont)

A beküldési határidő 2023. április 11-én LEJÁRT.

Megoldás. Még egy ilyen kitöltés:

A kitöltésben lévő számok összege 40.

Minden mezőre írunk számot a kitöltés során. A huszonöt mezőt összesen 40 szomszédsági oldalszakasz választja el. Minden ilyen oldalszakaszt pontosan egyszer számolunk meg: akkor, amikor a két mező közül a másodikat kitöltjük. Ezért lesz 40 a számok összege.

Statisztika:

155 dolgozat érkezett.
5 pontot kapott:	89 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	21 versenyző.
2 pontot kapott:	22 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	5 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2023. márciusi matematika feladatai