 |
A K/C. 763. feladat (2023. március) |
K/C. 763. Egy egységnyi sugarú félkörbe két olyan, az átmérőre illeszkedő négyzetet írunk, melyeknek van közös oldalszakasza, és egy-egy csúcsuk a körvonalra illeszkedik.

Tudjuk, hogy a kör középpontjából a két négyzet körön lévő csúcsaihoz húzott sugarak egymásra merőlegesek. Igazoljuk, hogy a két, ilyen módon megrajzolt négyzet területének összege állandó.
(5 pont)
A beküldési határidő 2023. április 11-én LEJÁRT.
1. megoldás. A négyzeteknek a félkörön levő csúcsait P-vel és Q-val jelöltük, ezeknek a pontoknak a félkör átmérőjére eső merőleges vetületei S, illetve T. A PS és QT szakaszok a négyzetek oldalai, ezeket a-val és b-vel, a kör középpontját K-val jelöltük.

1. ábra
A feladat megadja, hogy a két négyzetnek a félkörön lévő csúcsaihoz húzott sugarak egymásra merőlegesek. Az ábrán keletkező KPS és KQT derékszögű háromszögeknek a K csúcsnál levő hegyesszögei α és 90∘−α, így a két háromszög hasonló, és egyúttal egybevágó is, mert átfogójukra teljesül, hogy KP=KQ=1. Ezért a befogóik rendre megegyeznek, azaz KS=b és KT=a.
Így a Pitagorasz-tétel szerint
a2+b2=1.
A feltételeknek megfelelő négyzetek területének összege tehát valóban állandó és éppen a félkör egységnyi sugarának négyzetével egyenlő.
2. megoldás. Az 1. megoldás ábráját a KS=x, illetve KT=y jelölésekkel egészítjük ki az alábbi ábra szerint.

2. ábra
Írjuk fel a Pitagorasz-tételt a KPS és KQT derékszögű háromszögekre (az átfogó mindkét háromszögben a félkör egységnyi sugarával egyenlő hosszúságú):
a2+x2=1,
b2+y2=1.
Tudjuk még, hogy
x+y=a+b,
és így
a2+x2=b2+y2,
a2−b2=y2−x2,
(a+b)(a−b)=(y+x)(y−x).
Innen az x+y=a+b alapján egyrészt
a−b=y−x,
másrészt az a−b=y−x és a+b=x+y megfelelő oldalait összeadva
2a=2y,
ahonnan a=y és ezért b=x adódik.
Ebből az következik, hogy a két derékszögű háromszög egybevágó, a Pitagorasz-tételt felírva tehát
a2+b2=1.
Ezzel beláttuk, hogy a két négyzet területének összege állandó, és ez az állandó a félkör egységnyi sugarának négyzete.
3. megoldás. A négyzetek félkörön levő pontjait most is P-vel és Q-val, a megfelelő négyzetek oldalait a-val és b-vel, a félkör középpontját K-val jelöljük. Tükrözzük a félkört és a négyzeteket a félkör átmérőjének egyenesére, a P és Q pont tükörképei legyenek P′, illetve Q′.
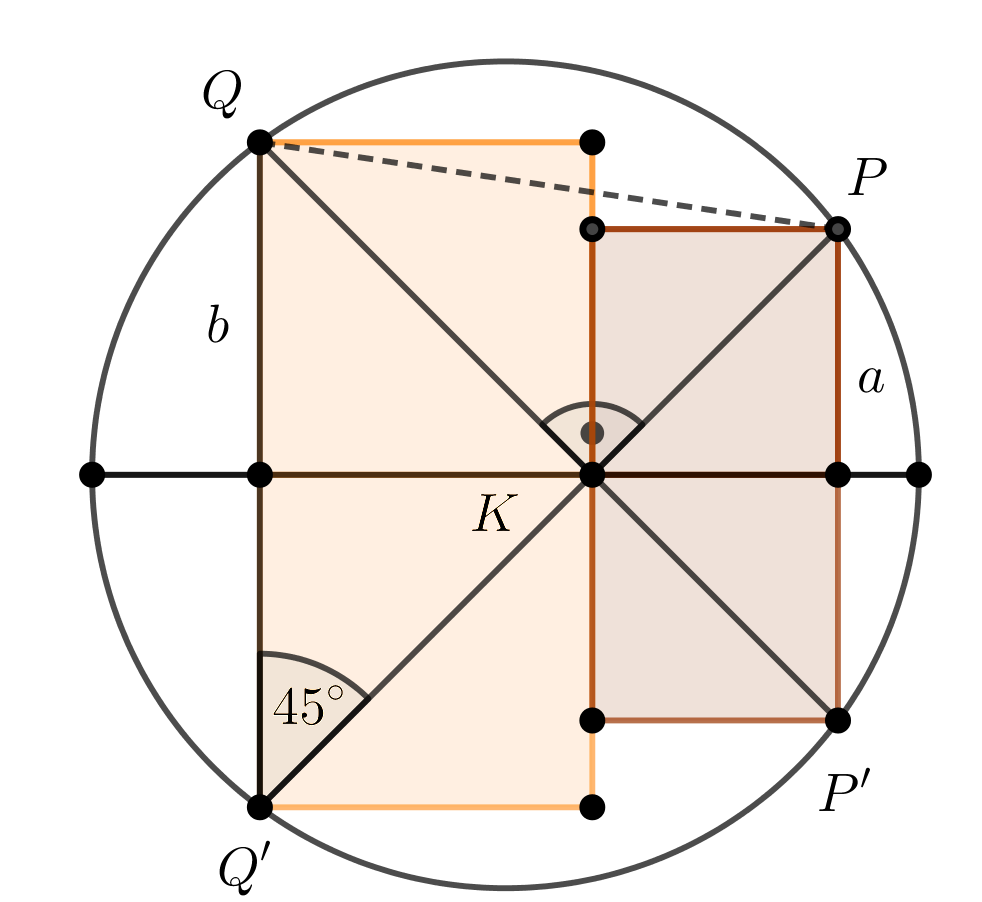
3. ábra
A feltétel szerint KP⊥KQ, ezért a tükrözés tulajdonságaiból KP′⊥KQ′ következik. Ugyancsak a tükrözés miatt kapjuk azt, hogy PQ′⊥QP′, és KQ′ a b oldalú négyzet tükörképének átlója, ezért
KQ′Q∢=45∘.
A PQ húr tehát egy 45∘-os kerületi szöghöz tartozó húr, így hossza a sugár √2-szöröse, azaz PQ=√2.
Ebből a KPQ derékszögre felírt Pitagorasz-tétel segítségével kapjuk, hogy
(a√2)2+(b√2)2=(√2)2,
hiszen KP=a√2 és KQ=b√2.
A műveletek elvégzésével és egyszerűsítéssel adódik, hogy
a2+b2=1.
Eszerint a két négyzet területének összege az egységnyi hosszúságú sugár négyzetével egyenlő, tehát valóban állandó.
Statisztika:
116 dolgozat érkezett. 5 pontot kapott: 57 versenyző. 4 pontot kapott: 21 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 3 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2023. márciusi matematika feladatai
|
|

