 |
A K/C. 802. feladat (2024. február) |
K/C. 802. Legyen az \(\displaystyle ABCD\) négyzet \(\displaystyle CD\) oldalának tetszőleges belső pontja \(\displaystyle Q\). Az \(\displaystyle AQ\) egyenesre állítsunk merőlegest a \(\displaystyle B\) csúcsból, legyen ennek \(\displaystyle AQ\)-val vett metszéspontja \(\displaystyle P\). Legyen továbbá a négyzet átlóinak metszéspontja \(\displaystyle K\). Mutassuk meg, hogy a \(\displaystyle PK\) egyenes felezi a \(\displaystyle QPB\) szöget.
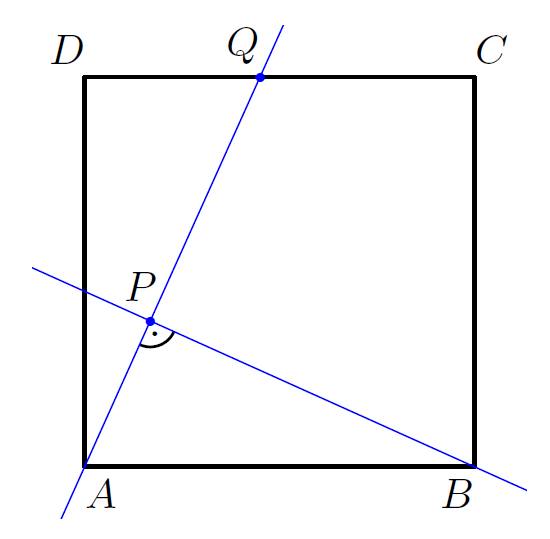
(5 pont)
A beküldési határidő 2024. március 11-én LEJÁRT.
Megoldás. A négyzet átlóinak \(\displaystyle K\) metszéspontja a négyzet szimmetriaközéppontja. Mivel \(\displaystyle Q\) a \(\displaystyle CD\) oldal belső pontja, ezért \(\displaystyle AQ\) biztosan nem megy át a \(\displaystyle K\) ponton, emiatt \(\displaystyle K\) nem illeszkedik a \(\displaystyle BP\) egyenesre sem. Tükrözzük az \(\displaystyle AQ\) és \(\displaystyle BP\) egyeneseket a \(\displaystyle K\) pontra. Tekintsük a következő ábrát, amelyen az \(\displaystyle AQ\) egyenesnek a \(\displaystyle BP\) egyenes tükörképével való metszéspontját \(\displaystyle R\)-rel, a \(\displaystyle BP\) egyenesnek a \(\displaystyle DA\)-val való metszéspontját \(\displaystyle S\)-sel, a megfelelő tükörképpontokat vesszővel jelöltük.

Mivel \(\displaystyle K\) nem illeszkedik az \(\displaystyle AQ\) egyenesre, ezért \(\displaystyle AQ\parallel CQ'\), hiszen \(\displaystyle A\) tükörképe \(\displaystyle C\). Hasonlóképpen a \(\displaystyle BS\) egyenesre sem illeszkedik \(\displaystyle K\), így \(\displaystyle BS\parallel DS'\), mivel \(\displaystyle B\)-nek \(\displaystyle K\)-ra vonatkozó tükörképe \(\displaystyle D\). Ez az \(\displaystyle APB\sphericalangle=90^{\circ}\) miatt azt jelenti, hogy a \(\displaystyle PR'P'R\) négyszög szögei derékszögek, tehát téglalap. Bizonyítani fogjuk, hogy \(\displaystyle PR'P'R\) négyzet.
A \(\displaystyle BSA\) és \(\displaystyle AQD\) derékszögű háromszögek egybevágók, mert \(\displaystyle ABS\sphericalangle\) és \(\displaystyle QAD\sphericalangle\) merőleges szárú hegyesszögek és így \(\displaystyle ASB\sphericalangle=AQD\sphericalangle\) is igaz, másrészt a megfelelő szögekkel szemközti \(\displaystyle AB\) és \(\displaystyle DA\) oldalak hossza egyenlő.
Ez azt is jelenti, hogy \(\displaystyle AS=DQ\) és ezért \(\displaystyle DS=CQ\). Az \(\displaystyle AQCQ'\) és \(\displaystyle DSBS'\) négyszögek a tükrözés miatt paralelogrammák, szögeik \(\displaystyle ASB\sphericalangle=AQD\sphericalangle\) miatt egyenlők, így \(\displaystyle DS=CQ\), illetve \(\displaystyle BS=AQ\) miatt a paralelogrammák egybevágók is. Eszerint az \(\displaystyle AQCQ'\) paralelogrammának az \(\displaystyle AQ\) oldalhoz tartozó magassága ugyanolyan hosszú, mint a \(\displaystyle DSBS'\) paralelogramma \(\displaystyle BS\) oldalához tartozó magassága, vagyis
\(\displaystyle PR'=PR,\)
ez éppen azt jelenti, hogy a \(\displaystyle PR'P'R\) téglalap négyzet, amelynek szimmetriaközéppontja \(\displaystyle K\). Ebből azonnal következik, hogy \(\displaystyle PK\) felezi a \(\displaystyle QPB\) derékszöget.
Statisztika:
A KöMaL 2024. februári matematika feladatai

