A K/C. 813. feladat (2024. április)

K/C. 813. Az $\displaystyle ABCD$ négyzet mellé rajzoltuk az $\displaystyle EBFG$ négyzetet, mellé pedig több, vele egybevágó négyzetet az alábbi ábra szerint.

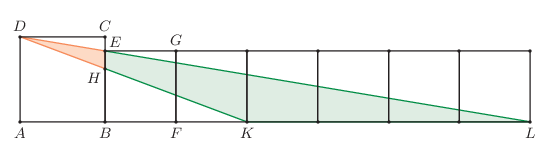
Határozzuk meg a $\displaystyle DHE$ háromszög és $\displaystyle HKLE$ négyszög területének arányát.

Deres János (Csurgó) ötletéből

(5 pont)

A beküldési határidő 2024. május 10-én LEJÁRT.

Megoldás. Használjuk a feladat szövegében szereplő ábrát és annak jelöléseit, továbbá jelöljük az $\displaystyle EBFG$ négyzet oldalát $\displaystyle a$-val, az $\displaystyle ABCD$ négyzet oldalát pedig $\displaystyle x$-szel. A $\displaystyle DCE \triangle$ hasonló az $\displaystyle LBE \triangle$-höz, mert szögeik páronként megegyeznek, ebből következően megfelelő oldalaikra igaz, hogy

$\displaystyle \frac{DC}{CE}=\frac{LB}{BE},$

$\displaystyle \frac{x}{CE}=\frac{6a}{a}.$

Tehát $\displaystyle \displaystyle{CE=\frac{x}{6}}$, vagyis $\displaystyle \displaystyle{EB=\frac{5}{6}x=a}$, azaz $\displaystyle \displaystyle{x=\frac{6}{5}a}$.

A $\displaystyle DAK \triangle$ hasonló a $\displaystyle HBK \triangle$-höz, mert szögeik páronként megegyeznek. Így tehát a megfelelő oldalak arányát felírva azt kapjuk, hogy

$\displaystyle \frac{DA}{AK}=\frac{HB}{BK},$

$\displaystyle \frac{\frac{6}{5}a}{\frac{6}{5}a+2a}=\frac{HB}{2a},$

$\displaystyle \frac{6}{5}\cdot \frac{5}{16}\cdot2a=HB,$

$\displaystyle \frac{3}{4}a=HB,$

vagyis $\displaystyle \displaystyle{EH=\frac{1}{4}a}.$ Ez alapján már felírhatjuk a $\displaystyle DHE$ és a $\displaystyle HKLE$ területét:

$\displaystyle T_{DHE}=\frac{EH\cdot x}{2}=\frac{\frac{1}{4}a\cdot \frac{6}{5}a}{2}=\frac{3}{20}a^2,$

$\displaystyle T_{HKLE}=T_{EBL}-T_{HBK}=\frac{6a\cdot a}{2}-\frac{2a\cdot \frac{3}{4}a}{2}=3a^2-\frac{3}{4}a^2=\frac{9}{4}a^2.$

A keresett arány pedig:

$\displaystyle \frac{T_{DHE}}{T_{HKLE}}=\frac{\frac{3}{20}a^2}{\frac{9}{4}a^2}=\frac{12}{180}=\frac{1}{15}.$

Statisztika:

87 dolgozat érkezett.
5 pontot kapott:	Aaishipragya Kahaly, Auer Sára, Barna 201 Krisztina, Bartusková Viktória, Beinschroth Máté, Blaskovics Ádám, Blaskovics Bálint, Budai Máté, Danka Emma, Domján István, Gáthi Donát, Hajnal Ákos Huba, Halmosi Dávid, Hetyei Dániel, Holczer Kenéz, Hollósi Dominik, Horvath Benedek, Horváth Imre, Juhász Zsombor, Kanalas Patrik, Kókai Ákos, Kószó Ferenc, Kovács Dániel, Kővágó Edit Gréta, Magyar Levente Árpád, Máté Kristóf, Mikó Hédi Irma, Mixtay Marcell, Mizsei Márton, Molnár Lili, Molnár-Sáska Tamás, Nelissen Sámuel Zalán, Németh Ábel, Olajos Anna, Páternoszter Tamás, Pázmándi Renáta , Rasztgyörgy Jázmin, Sipos Márton, Szabó András, Szabó Zétény Attila, Szalóki Árpád, Szilágyi Balázs , Tóth 207 Bence, Tóth Luca, Válek Péter, Viczián Adél.
4 pontot kapott:	11 versenyző.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	4 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	14 dolgozat.

A KöMaL 2024. áprilisi matematika feladatai