 |
A K/C. 818. feladat (2024. május) |
K/C. 818. Az ABC derékszögű háromszög befogóinak hossza BC=6, CA=8 egység. A BC befogó B-hez közelebb eső harmadolópontja P, felezőpontja Q, a CA befogó C-hez közelebbi harmadolópontja R, felezőpontja S, végül az AB átfogó A-hoz közelebbi harmadolópontja T, felezőpontja U. Tükrözzük a P, R, T harmadolópontokat az ABC háromszög hozzájuk legközelebb eső csúcspontjára, a Q, S, U felezőpontokat pedig a megfelelő háromszögoldal másik végpontjára az ábra szerint.
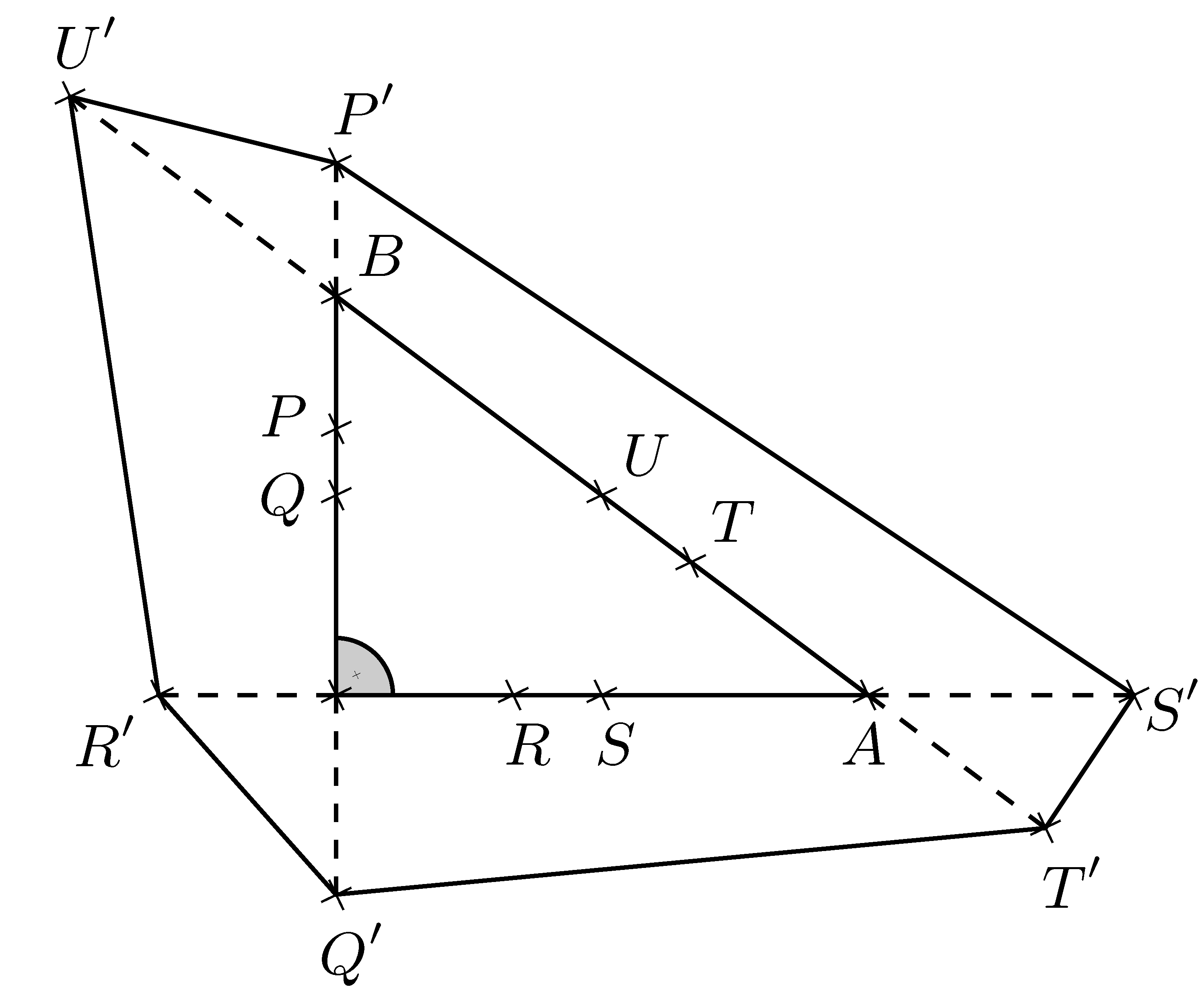
Határozzuk meg a P′U′R′Q′T′S′ sokszög területét.
Javasolta: Bíró Bálint, (Eger)
(5 pont)
A beküldési határidő 2024. június 10-én LEJÁRT.
Megoldás. Jelölje az ABC háromszög területét t. Az ABC derékszögű, két befogója 6 és 8, ezért területe: t=6⋅82=24. A P′U′R′Q′T′S′ hatszög területét úgy kapjuk meg, hogy kiszámoljuk és összeadjuk az alábbi háromszögek és négyszögek területét:
| (1) | TP′U′R′Q′T′S′=TABC+TBP′U′+TCR′Q′+TAT′S′+TBU′R′C+TCQ′T′A+TAS′P′B. |
A BP′U′ és a BPU háromszögben két-két oldal és az általuk bezárt szög megegyezik, ezért BPU△≅BP′U′△, így
| (2) | TBPU=TBP′U′. |
Ugyanezért CR′Q′△≅CRQ△ és AT′S′△≅ATS△, és TCRQ=TCR′Q′ és TATS=TAT′S′. Az alábbiakban azt fogjuk többször kihasználni, hogy ha két háromszögre teljesül, hogy egy-egy alapjuk ugyanazon az egyenesen van, és az ehhez tartozó magasságuk közös, akkor területük aránya az alapok arányával egyenlő. Például a BPU és a BCU háromszög BP és PC oldala egy egyenesen van, arányuk 1:3, az ezekhez tartozó, vagyis az U-ból induló magasságuk közös, ezért
| (3) | TBPU=13TBCU=TBP′U′. |
Ugyanígy felírhatjuk az összefüggést a BCU és az ABC területe közt annak alapján, hogy az U felezi az AB oldalt:
| (4) | TBCU=12t. |
A (2), a (3) és a (4) alapján tehát
TBP′U′=13⋅12⋅t=16t.
Hasonlóképp igaz, hogy
TCR′Q′=16tésTAT′S′=16t.
Az (1)-ből tehát az első négy tagot már megkaptuk. A további három tag három négyszög területe, ezek mindegykét vágjuk két-két háromszögre az U′C, a Q′A és az S′B szakaszok mentén. Ekkor igazak a következő összefüggések:
| (5) | TCBU′=3⋅TBP′U′=3⋅t6=t2(közös magasság és BC=3BP′ alapján), |
továbbáTCAU′=t+TCBU′=t+t2=32t,valamint
| (6) | TR′CU′=13⋅TCAU′=13⋅32t=t2(közös magasság és R′C=13CA alapján). |
(5) és (6) alapján pedig:
TBU′R′C=TCBU′+TR′CU′=t2+t2=t.
A maradék két tag is felírható ugyanilyen megfontolások alapján:
TCQ′T′A=TCQ′A+TQ′T′A=3TCR′Q′+13TBQ′T′=3⋅t6+13(t+TCQ′A)=t2+13(t+t2)=t2+t2=t.
TAS′P′B=TAS′B+TBS′P′=3TAT′S+13TCS′B=3⋅t6+13(t+TAS′B)=t2+13(t+t2)=t2+t2=t.
Így felírható a keresett terület:
TP′U′R′Q′T′S′=t+3⋅t6+3t=92t=92⋅24=108.
Statisztika:
71 dolgozat érkezett. 5 pontot kapott: Aaishipragya Kahaly, Auer Sára, Bartusková Viktória, Beinschroth Máté, Blaskovics Ádám, Blaskovics Bálint, Budai Máté, Danka Emma, Domján István, Fülöp Magdaléna, Gaál Gergely, Hajnal Ákos Huba, Hetyei Dániel, Horvath Benedek, Kószó Ferenc, Kökény Kristóf, Kun Petra, Magyar Levente Árpád, Máté Kristóf, Mikó Hédi Irma, Mizsei Márton, Molnár Lili, Molnár-Sáska Tamás, Németh Ábel, Olajos Anna, Pázmándi Renáta , Rasztgyörgy Jázmin, Sipos Márton, Szabó András, Szabó Máté, Szalóki Árpád, Tamás Attila Gábor, Tóth 207 Bence, Válek Péter, Viczián Adél. 4 pontot kapott: Hollósi Dominik, Juhász Zsombor, Kővágó Edit Gréta, Kulcsár Anna Zita, Li Mingdao, Tóth Luca. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 11 dolgozat.
A KöMaL 2024. májusi matematika feladatai
|
|

