A K/C. 827. feladat (2024. október)

K/C. 827. Egy hatszög minden szöge $\displaystyle 120^{\circ}$. Mutassuk meg, hogy bármelyik két szomszédos oldal összege megegyezik a szemben fekvő szomszédos oldalak hosszának összegével.

(5 pont)

A beküldési határidő 2024. november 11-én LEJÁRT.

Megoldás. Mivel a hatszög minden szöge $\displaystyle 120^{\circ}$, ezért a szemközti oldalai párhuzamosak.

Jelölje a hatszög csúcsait $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle D$, $\displaystyle E$ és $\displaystyle F$ az ábrán látható módon.

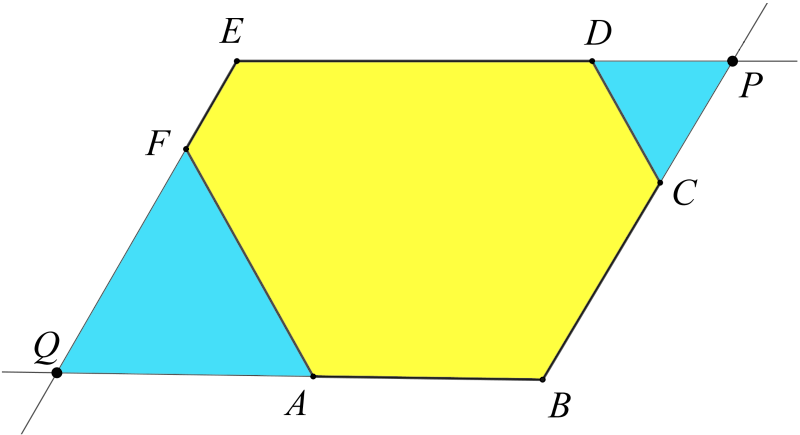
Az $\displaystyle ED$ és a $\displaystyle BC$ félegyenesek metszéspontját jelölje $\displaystyle P$, az $\displaystyle EF$ és $\displaystyle BA$ félegyenesekét $\displaystyle Q$. Mivel az $\displaystyle EQBP$ négyszög szemközti oldalai párhuzamosak, így az paralelogramma, tehát a szemközti oldalai egyenlőek. Például $\displaystyle QB=PE$, vagyis

Mivel az $\displaystyle FQA$ és $\displaystyle CPD$ háromszögek minden szöge 60°, ezért ezek szabályos háromszögek. Következésképp az egyes háromszögekben minden oldal egyenlő, például $\displaystyle QA=AF$ és $\displaystyle CD=PD$. E két egyenlőség és (1) alapján $\displaystyle FA+AB$=$\displaystyle CD+DE$, vagyis erre a négy oldalra teljesül a feladat állítása. Mivel ez a gondolatmenet bármely 2-2 szemben fekvő oldalra érvényes, így a feladat állítása igaz.

Statisztika:

271 dolgozat érkezett.
5 pontot kapott:	110 versenyző.
4 pontot kapott:	20 versenyző.
3 pontot kapott:	14 versenyző.
2 pontot kapott:	25 versenyző.
1 pontot kapott:	44 versenyző.
0 pontot kapott:	16 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	35 dolgozat.

A KöMaL 2024. októberi matematika feladatai