A K/C. 833. feladat (2024. november)

K/C. 833. Adott az ábra szerinti $\displaystyle {20~\mathrm{cm}\times 30~\mathrm{cm}}$ méretű, téglalap alakú papírlap. Az $\displaystyle A$ és $\displaystyle C$ csúcsát egymásra hajtva a hajtásegyenes a téglalap $\displaystyle AB$ és $\displaystyle CD$ oldalait a $\displaystyle P$ és $\displaystyle Q$ pontokban metszi. Mutassuk meg, hogy az $\displaystyle APCQ$ négyszög rombusz, és számoljuk ki a területét.

(5 pont)

A beküldési határidő 2024. december 10-én LEJÁRT.

Megoldás.

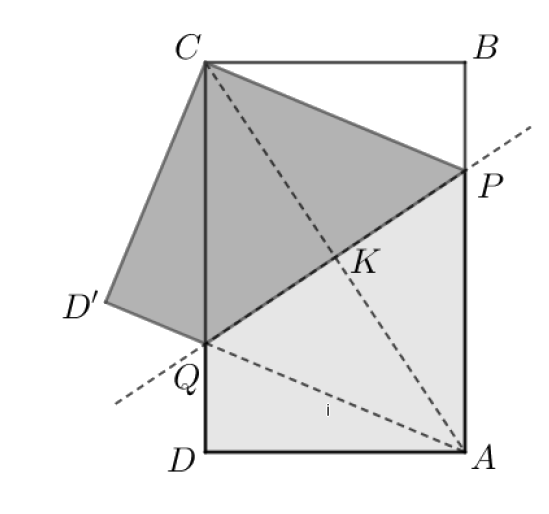
Az $\displaystyle A$ csúcs $\displaystyle C$ csúcsra hajtásakor a hajtásvonal merőlegesen felezi a $\displaystyle K$ pontban az $\displaystyle AC$ átlót, mert az $\displaystyle APQD$ négyszöget $\displaystyle PQ$-ra tengelyesen tükrözve kapjuk a $\displaystyle CPQD'$ négyszöget. Másrészt a $\displaystyle K$ ponton átmenő $\displaystyle PQ$ szakaszt is felezi a $\displaystyle K$ pont, mert a téglalap középpontosan szimmetrikus négyszög. Így $\displaystyle AKQ$, $\displaystyle AKP$, $\displaystyle CKP$ és $\displaystyle CKQ$ egybevágó derékszögű háromszögek, mert a befogóik páronként egyenlő hosszúak. Ezért az átfogóik is egyenlő nagyságúak, azaz $\displaystyle AQ=CQ=CP=AP$, tehát beláttuk, hogy az $\displaystyle APCQ$ négyszög rombusz.

Legyen $\displaystyle PB=x$, ekkor $\displaystyle AP=PC=30-x$. A $\displaystyle PCB$ derékszögű háromszögben felírva a Pitagorasz-tételt: $\displaystyle x^2+20^2=(30-x)^2$, ahonnan $\displaystyle x=25/3$, így a rombusz oldala $\displaystyle 30-25/3=65/3$ cm hosszú, területe pedig $\displaystyle T=65/3\cdot20=1300/3 \textrm{~cm}^2 \approx 433,33 \textrm{~cm}^2$.

Statisztika:

195 dolgozat érkezett.
5 pontot kapott:	70 versenyző.
4 pontot kapott:	30 versenyző.
3 pontot kapott:	21 versenyző.
2 pontot kapott:	26 versenyző.
1 pontot kapott:	9 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	30 dolgozat.

A KöMaL 2024. novemberi matematika feladatai