A K/C. 837. feladat (2024. december)

K/C. 837. Egy \(\displaystyle 4\times4\)-es táblázatot sakktáblaszerűen kiszínezünk. Egy lépésben egy kiszemelt \(\displaystyle 2\times2\)-es részen minden mező színét megváltoztatjuk: feketéből fehér, fehérből fekete lesz.

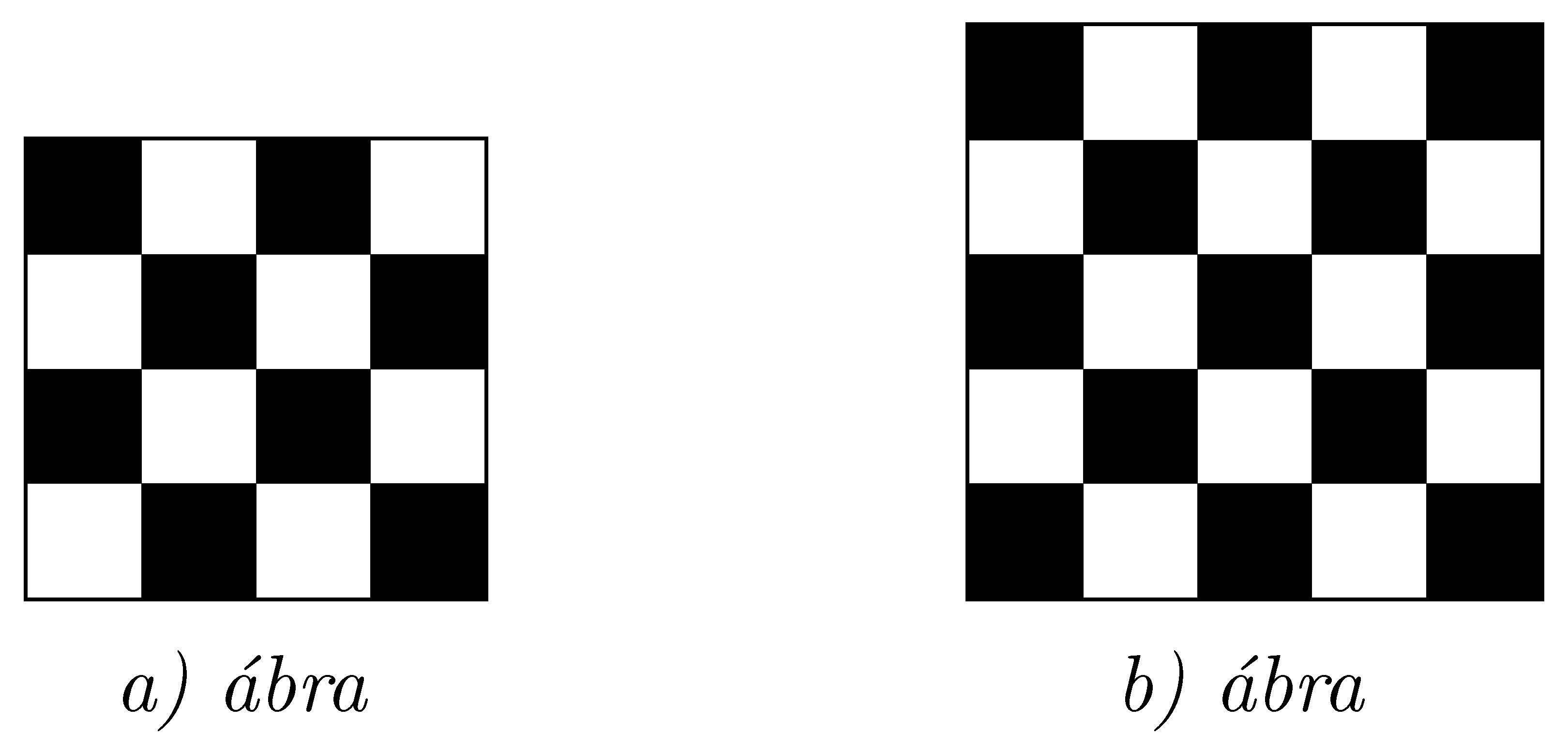
a) Megoldható-e így, hogy az egész tábla fekete színű legyen?

b) És egy \(\displaystyle 5\times5\)-ös tábla esetén elérhető-e, hogy az egész tábla fekete legyen?

(5 pont)

A beküldési határidő 2025. január 10-én LEJÁRT.

Megoldás. a) Igen, megoldható. Például így:

vagy például így:

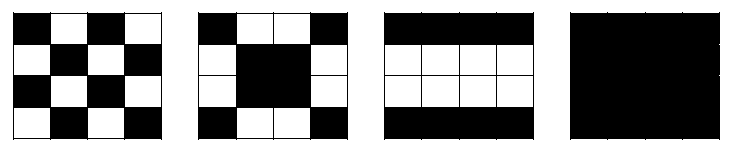
b) Az \(\displaystyle 5\times5\)-ös táblázat minden egyes \(\displaystyle 2\times2\)-es mezőjén végrehajthatjuk az átszínezést, de ezek sorrendjétől nem függ a végső állás, mert minden mezőre csak a körülötte lévő \(\displaystyle 2\times2\)-es részek változtatása hat. Egy-egy ilyen \(\displaystyle 2\times2\)-es részt vagy átszínezünk valamikor, vagy nem. Ha páros sokszor színeztük, akkor az olyan, mintha nem színeztük volna, ha pedig páratlan sokszor, akkor az olyan, mintha csak egyszer színeztük volna. Így a 16 db \(\displaystyle 2\times2\)-es rész mindegyikén tulajdonképpen vagy változtatunk egyszer vagy nem. Tulajdonképpen csak azt kell eldönteni minden egyes \(\displaystyle 2\times\)2-es részről, hogy átszínezzük-e, vagy nem.

Mivel a sarokmezők a kiindulási helyzetben feketék, így a sarkokban lévő \(\displaystyle 2\times2\)-es részeket nem színezhetjük át, hiszen a sarokmezők színét csak ezek tudják megváltoztatni. Például a felső sor balról második mezője most fehér és azt csak a felső, balról második \(\displaystyle 2\times2\)-es mező átszínezésével tudjuk feketévé változtatni, de ekkor a harmadik mező fehér lesz, amit csakis a felső, balról harmadik \(\displaystyle 2\times2\)-es mező átszínezésével tudunk visszafeketíteni. Ugyanígy az alsó sorban.

Az eddigi átszínezések ,,kötelezőek" voltak, ha a csupa fekete táblát szeretnénk elérni, az alábbi álláshoz jutunk:

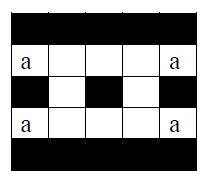
Most már csak a felső és alsó mezőket nem tartalmazó \(\displaystyle 2\times2\)-eseket színezhetjük át. Az a-val jelölt négy mezőt már csak egy-egy, őket tartalmazó (korábban nem átszínezett) \(\displaystyle 2\times2\)-es rész tartalmazza, így csakis ezek átszínezésével lehet őket feketévé változtatni, és ezt megtéve az alábbi színezést kapjuk:

Összesen négy \(\displaystyle 2\times2\)-es részt nem változtattunk meg, mégpedig azokat, melyek a táblázat középső mezőjét tartalmazzák. Ezek a középső \(\displaystyle 3\times3\)-as részen vannak. Ha bármelyiket átszínezzük, akkor ezzel együtt visszafehéredik egy-egy sarokmező ezen a \(\displaystyle 3\times3\)-as részen, melyek színén már változtatni a korábbiak alapján nem tudunk.

Így a teljesen fekete táblázatot elérni nem lehetséges.

Statisztika:

A K/C. 837. feladat értékelése még nem fejeződött be.

A KöMaL 2024. decemberi matematika feladatai