A K/C. 853. feladat (2025. március)

K/C. 853. Egy szabályos hatszög alapú egyenes hasáb alaplapjának élhossza $\displaystyle a$, magassága $\displaystyle b$. Tekintsük az összes alap- és oldallap minden átlója hosszainak összegét. Milyen $\displaystyle a:b$ arány esetén lesz ez az összeg $\displaystyle 12\bigl(a\sqrt{3}+3b\bigr)$?

Javasolta: Róka Bálint, Budapest

(5 pont)

A beküldési határidő 2025. április 10-én LEJÁRT.

Megoldás. Az alábbi ábrán az egyenes hasáb egy oldallapját, vagyis egy $\displaystyle a$, illetve $\displaystyle b$ oldalú téglalapot, valamint az alaplapját, tehát egy $\displaystyle a$ oldalú szabályos hatszöget ábrázoltunk.

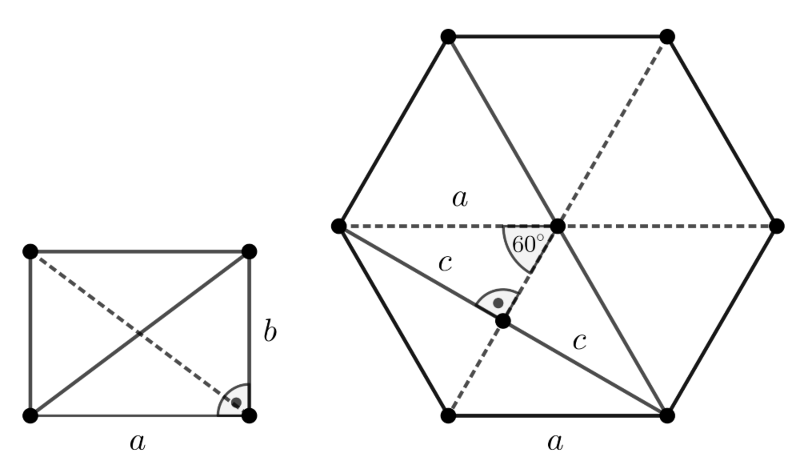
A hasáb palástját $\displaystyle 6$ darab, az ábrán megrajzolt egybevágó téglalap alkotja. A téglalapnak két átlója van, amelyek hossza a Pitagorasz-tétel miatt $\displaystyle \sqrt{a^2+b^2}$. A hasáb palástját alkotó $\displaystyle 6$ lap átlóinak összege ezért

A hasáb alapját jelentő szabályos hatszögnek összesen $\displaystyle \displaystyle{\frac{6\cdot3}{2}=9}$ átlója van. A hatszög egy csúcsából kétféle hosszúságú átló indul ki, két rövidebb, amelyek hossza a hatszög szimmetriája miatt egyenlő, és egy hosszabb. Az utóbbi átló hossza nyilvánvalóan $\displaystyle 2a$, hiszen a hatszöget hat darab $\displaystyle a$ oldalú szabályos háromszög alkotja, és mivel a $\displaystyle 2a$ hosszúságú átlóból a szabályos hatszögben $\displaystyle 3$ van, így azok összes hossza $\displaystyle 6a$.

Ha a rövidebb átló hosszát $\displaystyle 2c$-vel jelöljük, akkor a hatszög két szomszédos szabályos háromszögének közös oldala ezt az átlót merőlegesen felezi, így kapjuk az ábrán látható derékszögű háromszöget, amelynek átfogója $\displaystyle a$, a $\displaystyle 60^{\circ}$-os szöggel szemben fekvő befogója $\displaystyle c$ hosszúságú. Ez a derékszögű háromszög egy szabályos háromszög fele, ezért $\displaystyle \displaystyle{c=\frac{a}{2}\sqrt{3}}$, tehát $\displaystyle 2c=a\sqrt{3}$.

A $\displaystyle 2c$ hosszúságú rövidebb átlóból a szabáyos hatszögben összesen $\displaystyle 6$ darab van, így ezek összes hossza $\displaystyle 6a\sqrt{3}$.

Mivel a hasábnak két egybevágó szabályos hatszög alaplapja van, ezért ezek összes átlóinak hosszát összeadva a

értéket kapjuk.

Így az összes alap- és oldallap minden átlója hosszainak összege (1) és (2) figyelembevételével

Már csak arra kell válaszolnunk, hogy a (3) összeg milyen $\displaystyle \displaystyle{\frac{a}{b}}$ arány mellett lesz $\displaystyle 12\big(a\sqrt{3}+3b\big)$-vel egyenlő.

A $\displaystyle 12\big(\sqrt{a^2+b^2}+a+a\sqrt{3}\big)=12\big(a\sqrt{3}+3b\big)$ egyenlőségből $\displaystyle 12$-vel való osztás és rendezés után a

$\displaystyle \sqrt{a^2+b^2}=3b-a$

összefüggést kapjuk, ahol $\displaystyle 3b-a>0$ kell hogy legyen. Innen négyzetreemeléssel adódik, hogy $\displaystyle a^2+b^2=9b^2-6ba+a^2$.

Rendezéssel és egyszerűsítéssel:

$\displaystyle 3a=4b.$

Ez azt jelenti, hogy a hasáb összes lapja minden átlójának hosszát összeadva akkor kaphatunk $\displaystyle 12\big(a\sqrt{3}+3b\big)$ értéket, ha a hasáb $\displaystyle a$ alapélének és $\displaystyle b$ magasságának aránya $\displaystyle \displaystyle{\frac{a}{b}=\frac{4}{3}}$.

Megjegyzés. Az $\displaystyle \displaystyle{\frac{a}{b}=\frac{4}{3}}$ arányból következő $\displaystyle \displaystyle{a=\frac{4}{3}b}$ mellett a $\displaystyle \sqrt{a^2+b^2}=3b-a$ egyenlet mindkét oldalának értéke $\displaystyle \displaystyle{\frac{5}{3}b}$.
Ez megfelel a $\displaystyle 3b-a>0$ feltételnek.

Statisztika:

159 dolgozat érkezett.
5 pontot kapott:	Aaishipragya Kahaly, Békési Máté, Farkas Noémi , Hajnal Ákos Huba, Kovács Domonkos, Papp Máté Milán, Szmodics Emese Anna.
4 pontot kapott:	107 versenyző.
3 pontot kapott:	13 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	20 dolgozat.

A KöMaL 2025. márciusi matematika feladatai