 |
A K. 112. feladat (2007. január) |
K. 112. A következő helyes összeadás minden sorából töröltünk egy-egy számjegyet, a megmaradt számokat összetoltuk egy-egy háromjegyű számmá és az összeadás helyes maradt. Ezután ugyanígy képeztünk kétjegyű számokat, majd egyjegyűeket és az összeadás mindkét lépésben helyes maradt. Melyek lehettek az egyes lépésekben eltávolított számok? Adjuk meg az összes lehetőséget.
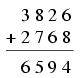
(6 pont)
A beküldési határidő 2007. február 15-én LEJÁRT.
Megoldás: Ha az első sorból törlünk egy számjegyet, akkor a kapott háromjegyű szám 3-mal vagy 8-cal kezdődik, és 2-re vagy 6-ra végződik. Ha a második sornál ugyanezt megtesszük, akkor a kapott háromjegyű szám 2-vel vagy 7-tel kezdődik, és 6-ra vagy 8-ra végződik. Figyelembe véve, hogy a két megmaradt háromjegyű szám összege is háromjegyű, a két háromjegyű szám első számjegye nem lehet 3-7, 8-2, 8-7, tehát csak a 3 és 2 állhat ezekben elöl. A háromjegyű számok végződései lehetnek 2-6, 2-8, 6-6, 6-8, ezekhez az összegben rendre a 8, 0, 2, 4 végződések tartoznak, amelyek közül csak a 4 jöhet szóba, az eredeti összeg számjegyeit tekintve. Tehát az első sorból a 8 vagy a 2, a második sorból pedig a 7 vagy a 6 lett törölve az első lépésben. Ha az ennek nyomán kialakuló 4 lehetőséget megvizsgáljuk, akkor továbblépést jelent a 326+268=594, illetve a 386+268=654 párosítás, a másik két esetben nem jön létre olyan összeg, mely a feltételeknek megfelelően állítható elő. Tekintsük először a 326+268=594 esetet. Itt a keletkező kétjegyű számok lehetséges végződései megegyeznek az eredeti lehetséges végződésekkel, tehát az összeg lehetséges végződései is, emiatt a háromjegyű számok utolsó számjegye nem törölhető. Megint 4 esetet kaptunk a törölt számjegypárokra, melyeket megvizsgálva A 26+68=94 és a 26+28=54 ad lehetséges továbblépést. Viszont az elsőből már nem tudunk úgy számjegyeket törölni, hogy a feltételt teljesítsük, a másodikból viszont igen: 2+2=4. Tekintsük most a 386+268=654 esetet. Az első számból a 3 nem törölhető, mert akkor a kapott kétjegyű számok összege 100-nál mindenképp több lenne, így az első számból maradhat 36 vagy 38. A második számból ennek megfelelően a 2 szintén nem törölhető, tehát ebből 26 vagy 28 lesz. Az összeg lehetséges végződése 5 vagy 4, ezért csak a 36+28, vagy a 38+26 párosítás jöhet szóba, az előbbi nem jó, az utóbbi összeg 64. Itt viszont már nem törölhető még egy számjegy a feltételeknek megfelelően. Tehát az egyetlen lehetséges megoldás a törölt számokra: 8,7,6; majd 3,6,9; majd 6,8,5.
Értékelés:
6 pontot az kapott, aki világosan, érthetően leírta, hogy a feladatnak miért 1 megoldása van. Ez azt jelenti, hogy pontosan indokolta, hogy miért csak 2 háromjegyű, azokból 4 kétjegyű, és azokból 1 egyjegyű összeadás valósítható meg.
5 pontot a fentiekhez hasonló szintű, kissé hiányos dolgozatokra adtunk.
4 pontot a fent említett hét összeadás folyamatábráját, de indoklást nem tartalamzó dolgozatra adtunk.
3 pontos az a dolgozat, amelyikben az előzőekhez képest még több hiba van.
2 pontos a végeredményet megadó dolgozat.
1,, ill. 0 pontos a bármilyen értékelhető észrevételt tartalmazó dolgozat, illetve a teljesen hibás dolgozat.
Statisztika:
154 dolgozat érkezett. 6 pontot kapott: Balla Regina, Bódis Attila, Bognár Barna, Budai Barbara, Csábi Barnabás, Csenger Tibor, Csere Kálmán, Donovál 128 Krisztina, Dömötör Krisztián, Fialowski Melinda, Ficzere Zsófia, Garamszegi Balázs, Harangozó Klára, Herczeg Mónika, Kiss Dávid, Kitzinger Andor, Kocsis 007 Bence, Kókai Mariann, Konczi Anita, Kovács 729 Gergely, Kovács Anita, Köteles István, Lajtai Krisztina, Losonczki Tamás, Major Bálint István, Mihálka Éva Zsuzsanna, Minya Fanni, Nagy Róbert, Najbauer Eszter Éva, Nánai Bálint, Ölvedi Balázs, Pálinkó Márton, Pasztuhov Anna, Poócza Eszter, Rákos Szilárd, Sárvári János, Scharle András, Szeifert Bea, Székely Anna Krisztina, Szepesvári Eszter, Széplaki Zita, Szögi Melinda, Tóth 004 Tamás, Tóth 943 Tímea, Török 162 Zsolt, Túri Attila, Varju 105 Tamás, Welsz Edit. 5 pontot kapott: 23 versenyző. 4 pontot kapott: 32 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 39 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2007. januári matematika feladatai
