 |
A K. 170. feladat (2008. szeptember) |
K. 170. Egy hosszú szalagra az ábrán látható, zárt töröttvonalból álló mintát nyomtatták. (Itt csak a szalag elejét és végét szemléltetjük.) A töröttvonal minden szakaszának hossza 1 cm.
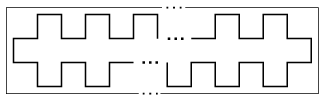
a) Lehet-e a szalagon levő minta hossza pontosan 100 cm?
b) Lehet-e a mintában látható szakaszok hosszának összege 2008 cm?
c) Hány cm hosszú részt foglal el a minta a szalagon, ha a minta által határolt terület nagysága 65 cm2?
(6 pont)
A beküldési határidő 2008. október 10-én LEJÁRT.
Megoldás. a) Mivel a mintában felváltva következnek egymás után 1 cm2 és 3 cm2 területű részek, továbbá az elején és a végén is 1-1 cm2-es rész található, ezért a minta hossza csak páratlan szám lehet, így 100 cm nem.
b) A minta lerajzolásakor a következő elvet követhetjük: 1. A bal oldalán kezdve rajzoljunk függőlegesen egy 1 cm-es szakaszt. 2. Ehhez hozzárajzoljuk a következő, összesen 8 cm-es vonaldarabokat, amit többször megismételünk. 3. Végül egy 3 cm-es vonaldarabbal lezárjuk a rajzot a másik végén.

Ennek megfelelően a szakaszok együttes hossza cm-ben mérve 8 valamely többszörösénél 4-gyel több. Mivel a 2008 osztható 8-cal, ezért a szakaszok összes hossza nem lehet 2008.
c) Mivel a 65 egységnyi területet a b) pontban leírt módon 16-szor a 2-es, majd a 3-as lépést végrehajtva érhetjük el, ezért a 2-es típusú lépésekkel 16.2=32 cm távolságra jutottunk el, majd a 3-as lépéssel még 1 cm-t haladtunk. Így a minta a szalagon 33 cm hosszú helyet foglal el.
Statisztika:
297 dolgozat érkezett. 6 pontot kapott: 57 versenyző. 5 pontot kapott: 50 versenyző. 4 pontot kapott: 37 versenyző. 3 pontot kapott: 34 versenyző. 2 pontot kapott: 34 versenyző. 1 pontot kapott: 28 versenyző. 0 pontot kapott: 41 versenyző. Nem versenyszerű: 16 dolgozat.
A KöMaL 2008. szeptemberi matematika feladatai
|
|

