A K. 209. feladat (2009. március)

K. 209. Egy kereskedő a fagylaltárusító pavilonjára körbe falemezből készült árnyékoló előtetőt szeretne szereltetni. Az előtetővel ellátott pavilon látszati és felülnézeti képét az ábrán láthatjuk. Az előtető egy-egy darabjának síkja a pavilon megfelelő függőleges oldalfalával 45^o-os szöget zár be. A pavilon alapja 3 m oldalhosszúságú négyzet. Az előtető a fal síkjától merőlegesen számított 1 m távolságig nyúlik ki. Hány m² falemez kell az előtető elkészítéséhez?

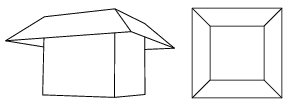
(6 pont)

A beküldési határidő 2009. április 10-én LEJÁRT.

Megoldás. Tekintsük az előtető egy darabját.

Ez egy szimmetrikus trapéz, melynek egyik alapja 3 m, így a másik alapja 3+2^.1=5 m (mert az előtető a fal síkjától 1 méterig nyúlik ki).

A trapéz magassága megegyezik egy 1 befogójú, egyenlő szárú derékszögű háromszög átfogójával (hiszen az előtető és az oldalfal által bezárt szög 45^o), vagyis $\sqrt2$ . Így a trapéz szára a Pitagorasz-tétel szerint $\sqrt3$ .

Így az előtető készítéséhez

$4\cdot\frac{(5+3)\sqrt2}{2}=16\sqrt2\approx22,6274~{\rm m}^2$

falemez kell.

Statisztika:

114 dolgozat érkezett.

6 pontot kapott: 59 versenyző.

5 pontot kapott: 3 versenyző.

4 pontot kapott: 8 versenyző.

3 pontot kapott: 17 versenyző.

2 pontot kapott: 15 versenyző.

0 pontot kapott: 1 versenyző.

Nem versenyszerű: 11 dolgozat.

A KöMaL 2009. márciusi matematika feladatai

114 dolgozat érkezett.
6 pontot kapott:	59 versenyző.
5 pontot kapott:	3 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	17 versenyző.
2 pontot kapott:	15 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	11 dolgozat.

Már regisztráltál?
Új vendég vagy?