A K. 217. feladat (2009. október)

K. 217. Egy négyzetrácsos játékterületen háromféle bombát helyezhetünk el. A bombák felrobbantásukkor saját mezőjüket, valamint az őket körülvevő mezőket (és azok tartalmát) robbantják fel. Az ábra azt mutatja, hogy a háromféle bomba milyen hatókörben robbantja fel a játékmezőket (a bombák helyét és típusát az ábrákban látható számok jelzik). Ha egy bomba által felrobbantott mező egy másik bombát tartalmaz, akkor az is fel fog robbanni, és hatósugarának megfelelően esetlegesen további mezőket robbant fel. Helyezzünk el 2-2 db 1-es, 2-es és 3-as típusú bombát egy játékmezőn úgy, hogy közülük valamelyiket felrobbantva minél több mező robbanjon fel.

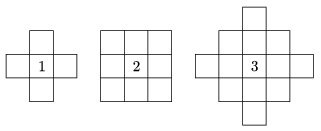
(6 pont)

A beküldési határidő 2009. november 10-én LEJÁRT.

Megoldás. A bombák hatósugarába eső területek átfedik egymást, ha láncreakció szerint szeretnénk felrobbantani őket. A közös mezők számát az alábbi táblázatban foglaljuk össze. A táblázat nem szimmetrikus, ha nem kölcsönösen robbantják fel egymást a bombák. Ebben az esetben a sorokban az először felrobbanó (ok), az oszlopokban az általuk felrobbantott bombatípusok vannak. A második táblázatban az egymást kölcsönösen felrobbantó bombák közös mezőinek minimális száma szerepel.

Mivel egy bomba felrobbantása újabb mezők, vagy újabb bomba felrobbantását jelenti, célunk az összes bomba felrobbantása. Legyen az \(\displaystyle i.\) bomba és az általa felrobbantott mezők területe összesen \(\displaystyle t_i\), az \(\displaystyle i.\) és \(\displaystyle j.\) bomba által közösen lefedett (felrobbantott) terület \(\displaystyle k_{ij}\). Ekkor együtt \(\displaystyle t_i+t_j-k_{ij}\) mezőt robbantanak fel. Ha ezek együtt felrobbantják az \(\displaystyle m.\) bombát, akkor a bombák alakja miatt biztos, hogy az \(\displaystyle i.\) és a \(\displaystyle j.\) küzül kiválasztható az egyik, mellyel az \(\displaystyle m.\) közös hatóterülettel rendelkezik és a másik -a közös területen kívülivel- nem. Ha ez az \(\displaystyle i.\), akkor a három közösen felrobbantott területe \(\displaystyle t_i+t_j-k_{ij}+t_m-k_{im}\), és így tovább. Tehát a felrobbantott terület a bombák összterületének az átfedésekkel való csökkentésével számolható. A bombák összesen külön-külön \(\displaystyle 2(5+9+13)=54\) mezőt fednek le. A kölcsönös felrobbantáshoz kell egy láncot találni, és a célunk, hogy ez lánc a legkisebb összátfedést adja.

A cél tehát, hogy a lánc-robbanások által minél kevesebb legyen a közös hatóterület. Minden bombának fel kell robbania, tehát valamelyik bomba okozza a másik robbanását (az elsőt kivéve): a táblázatban keressük azon öt számot, melyek összege a legkisebb, és egy oszlopból legfeljebb kettőt választhatunk. Ezen számok a \(\displaystyle 2, 2, 4, 4, 5\), összegük \(\displaystyle 17\). Az összesen felrobbantott terület \(\displaystyle 54-17=\mathbf{37}\). A táblázatbeli mezők kiválasztásával a bombák egymás után sorba fűzhetőek.

Megjegyzés: Ha bármelyik bomba felrobbantásával elpusztított mezők maximális számát keressük, akkor a következőt tehetjük. A második táblázat alapján az azonos típusú bombák robbantják fel egymást a legkevesebb átfedéssel, továbbá mivel az 1 és 2 átfedés kisebb mint 1 és 3-as, a legnagyobb pedig a 2 és 3-as, ezért a következő lánc lesz az optimális: \(\displaystyle 3a - 3b - 1a - 1b - 2a - 2b\), az összes átfedés pedig \(\displaystyle 5+5+2+4+4=20\), tehát a felrobbantott mezők száma \(\displaystyle 34\).

Statisztika:

240 dolgozat érkezett.
6 pontot kapott:	67 versenyző.
5 pontot kapott:	12 versenyző.
4 pontot kapott:	10 versenyző.
3 pontot kapott:	9 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	51 versenyző.
0 pontot kapott:	63 versenyző.
Nem versenyszerű:	15 dolgozat.

A KöMaL 2009. októberi matematika feladatai