A K. 259. feladat (2010. október)

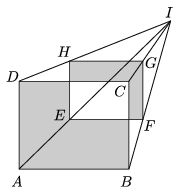
K. 259. Az ABCD és EFGH olyan egy síkban fekvő téglalapok, melyek oldalai párhuzamosak. Tudjuk, hogy AB=15 cm, AD=12 cm, EF=10 cm, EH=8 cm, FI=14 cm. Számítsuk ki a besatírozott részek területének különbségét.

(6 pont)

A beküldési határidő 2010. november 10-én LEJÁRT.

Megoldás. Az \(\displaystyle ABCD\) téglalap satírozott részének területét jelölje \(\displaystyle T_s\), az \(\displaystyle EFGH\) téglalap satírozott részének területét pedig \(\displaystyle t\). A téglalapok közös része szintén téglalap, melynek területe \(\displaystyle \tau\). Ekkor \(\displaystyle T-t=T+\tau -\tau -t=T_{ABCD}-T_{EFGH}=15\cdot 12 -10\cdot 8=80\). A satírozott síkidokok területének különbsége 80.

Statisztika:

218 dolgozat érkezett.
6 pontot kapott:	134 versenyző.
5 pontot kapott:	37 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	10 dolgozat.

A KöMaL 2010. októberi matematika feladatai