A K. 278. feladat (2011. január)

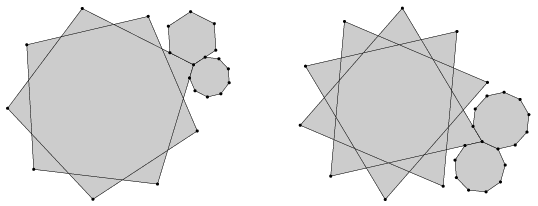
K. 278. Az alábbi két ábrán szabályos sokszögek (most megengedjük a csillagsokszögeket is) vannak összeillesztve egy-egy csúcsuknál. Tényleg mindkét esetben illeszkednek a sokszögoldalak egymásra, vagy valamelyik ábra ,,csal''?

(6 pont)

A beküldési határidő 2011. február 10-én LEJÁRT.

Megoldás. Az első ábrában a csillag-kilenc-szög oldalainak metszéspontjai egy szabályos kilencszöget alkotnak (forgás-szimmetria miatt), ezért az egymást metsző oldalak egymással $\displaystyle 140^\circ$-os szöget zárnak be. A csillagszög csúcsa és a vele szemközti oldalon levő két oldalmetszéspont alkotta háromszög szögei ezért $\displaystyle 40^\circ, 40^\circ, 100^\circ$. A szabályos hatszög szögei $\displaystyle 120^\circ$, továbbá a szabályos kilencszög szögei $\displaystyle 140^\circ$. A közös csúcsban egymáshoz csatlakoztatva sorban a sokszögek oldalait egy szögtartományt határoznak meg. Ha ez a szög teljes szög, akkor az ábra nem csal. Mivel $\displaystyle 100^\circ+120^\circ+140^\circ=360^\circ$, ezért az első ábra nem csal.

A második ábrán egy csillag-tízszöget használtak. Az oldalak metszéspontjai közül az a 10, mely a sokszög középpontjához legközelebb van, egy szabályos tízszöget alkot, melynek szögei $\displaystyle 144^\circ$. Ezen tízszög oldalegyenesei tehát $\displaystyle 36^\circ$-os szöget zárnak be egymással. Egy oldalegyenes és az őt $\displaystyle 36^\circ$-ban metsző két másik oldal alkotta háromszög harmadik szöge ezért $\displaystyle 108^\circ$. (Ezen oldalak metszéspontjai, melyek távolab vannak a szabályos tízszöget alkotóknál, de közelebb, mint az eredeti csillagtízszög csúcsai egy csillagtízszöget alkotnak $\displaystyle 108^\circ$-os szögekkel.) Az eredeti csillagtízszög egy csúcsával szemközti két oldal és a csúcsból induló két oldal egy deltoidot határoznak meg, melynek három szöge ismert: $\displaystyle 144^\circ, 72^\circ, 72^\circ$. Ezért az eredeti csillagtízszög szöge $\displaystyle 72^\circ$. A szabályos tízszög szöge $\displaystyle 144^\circ$, a szabályos kilencszög szöge pedig $\displaystyle 140^\circ$. Összegük $\displaystyle 366^\circ$, ami több, mint egy teljes szög, ezért az ábra csal, mert egy csúcs mentén egymás után illesztve a sokszögeket egymásba fognak lógni.

Statisztika:

164 dolgozat érkezett.
6 pontot kapott:	100 versenyző.
5 pontot kapott:	23 versenyző.
4 pontot kapott:	21 versenyző.
3 pontot kapott:	5 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	5 versenyző.
Nem versenyszerű:	7 dolgozat.

A KöMaL 2011. januári matematika feladatai