A K. 281. feladat (2011. január)

K. 281. Dominikának olyan dominókészlete van, amiben a legkisebb dominó a dupla 1-es, a legnagyobb a dupla 6-os, és közte minden párosításból 1 db van. Dominika rájött, hogy a dominókkal bizonyos törtszámokat is szemléltethet, ha a felső félen lévő szám a számláló, az alsó félen lévő a nevező. Dominika leült húgával, Noémival szemben, és az itt látható osztást rakta ki dominókból.

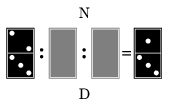
(6 pont)

A beküldési határidő 2011. február 10-én LEJÁRT.

Megoldás. A lefordított dominókon levő pöttyök száma legyen $\displaystyle a$ és $\displaystyle b$, illetve $\displaystyle c$ és $\displaystyle d$ (egészek, legalább 1, legfeljebb 6), amivel Dominika a $\displaystyle \displaystyle{\frac 23 : \frac ab : \frac cd = \frac 13}$ egyenlőséget látta, illetve Noémi felől $\displaystyle \displaystyle{\frac 31 = \frac dc : \frac ba : \frac 32}$-t. Az osztást elvégezve és átrendezve $\displaystyle 2bd=3ac$ és $\displaystyle 9bc=2ad$ összefüggéseket kapunk. A kettő hányadosa $\displaystyle \frac 92 \frac cd = 2\frac dc$, ahonnan $\displaystyle \frac dc=\frac 32$. Ez két módon lehetséges: $\displaystyle d=3$ és $\displaystyle c=2$ vagy $\displaystyle d=6$ és $\displaystyle c=4$. Ezt visszahelyettesítve $\displaystyle \frac ab=3$-t kapjuk, ahonnan $\displaystyle a=3$ és $\displaystyle b=1$ vagy $\displaystyle a=6$ és $\displaystyle b=2$. Mivel minden párból csak egy dominó van, ezért a megoldások közül a 2-3 és 1-3 pöttypárok nem lehetnek. Tehát a lefordított dominókon 6-2 illetve 4-6 pötty volt.

Statisztika:

151 dolgozat érkezett.
6 pontot kapott:	Arnold Balázs, Árvay Júlia, Bali Luca, Balogh Tamás, Csibi Levente, Déri Tamás, Domucza Katalin, Farkas Dóra, Fehér Gábor, Fülöp Zsófia, Halasi-Czalbert Pál, Hegedüs 222 Dániel, Jónás Judit, Katona Adrienn, Kecskeméti Ádám, Kerner Bálint, Kovács Norbert Krisztián, Kulcsár Ildikó, Lőrinczy Zsófia Noémi, Makk László, Marx Pál Fülöp, Móricz Tamás, Nemes Barnabás, Németh Klára Anna, Nguyen Tien Nam, Olajos Márton, Pogány Zsombor, Potyondi Gergő, Rácz 413 Bence, Rikker Bálint, Roósz Péter, Rovó Judit, Somogyvári Kristóf, Szabó 524 Tímea, Székely Ádám, Telek Máté László, Tihanyi Dániel, Tóth 095 Zsombor, Tóth Kristóf, Tőkés Anna, Varkoly Fanni, Várkonyi Balázs, Vörös Zoltán János, Werkmann Virág Anna.
5 pontot kapott:	25 versenyző.
4 pontot kapott:	18 versenyző.
3 pontot kapott:	18 versenyző.
2 pontot kapott:	22 versenyző.
1 pontot kapott:	18 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2011. januári matematika feladatai