A K. 303. feladat (2011. október)

K. 303. Hány darab háromszöget, rombuszt és húrtrapézt találhatunk az ábrán?

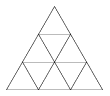
(6 pont)

A beküldési határidő 2011. november 10-én LEJÁRT.

Megoldás. Rombuszból csak egyféle van (l. ábra): összesen 9 db található belőle az ábrán (az alsó sorban kettő balra, kettő jobbra fordulva, ugyanez minden oldalon, de a csúcsoknál levőket kétszer számoltuk, így 12–3=9 a teljes darabszám).

Háromszögből háromféle van, a legkisebből 9 db, a közepes méretűből 3 db, a legnagyobból pedig 1 db van, összesen 13 db.

Trapézból is háromféle van: a legkisebből 12 db van (egy oldallal párhuzamos alapokkal rendelkezőből az oldalon van három: kettő az ábrán látható helyzetben, egy pedig fejjel lefelé, és a középső sorban is van egy talpon állva), a közepes és a nagy méretűből is összesen 3-3 db van, összesen 18 db.

Tehát trapézból van a legtöbb.

Statisztika:

331 dolgozat érkezett.
6 pontot kapott:	88 versenyző.
5 pontot kapott:	13 versenyző.
4 pontot kapott:	102 versenyző.
3 pontot kapott:	29 versenyző.
2 pontot kapott:	66 versenyző.
1 pontot kapott:	21 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2011. októberi matematika feladatai