A K. 304. feladat (2011. október)

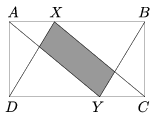
K. 304. Az ABCD téglalap AB oldalának harmadolópontja X, CD oldalának harmadolópontja Y az ábrának megfelelően. Határozzuk meg, hogy az ábrán szürkével jelölt síkidom területe hányadrésze az ABCD téglalap területének.

(6 pont)

A beküldési határidő 2011. november 10-én LEJÁRT.

Megoldás. Az ábra szimmetriája miatt a satírozott négyszög paralelogramma. Rajzoljuk be ennek \(\displaystyle XY\) átlóját! Ez az átló felezi a paralelogramma területét. Az \(\displaystyle AXY\) háromszög területe az \(\displaystyle ABCD\) téglalap területének hatodrésze (alapja az \(\displaystyle AB\) harmadrésze, magassága \(\displaystyle BC\)). A \(\displaystyle DYZ\) háromszög oldalai kétszer akkorák, mint az \(\displaystyle AXZ\) háromszögé, mert a két háromszög hasonló. Így \(\displaystyle Z\) az \(\displaystyle AY\) szakasz harmadolópontja, ezért az \(\displaystyle XYZ\) háromszög területe az \(\displaystyle AXY\) háromszög területének kétharmada. Tehát az \(\displaystyle XYZ\) háromszög területe a téglalap területének hatodának kétharmada, azaz egykilencede. A paralelogramma területe ennek kétszerese, vagyis a téglalap területének 2/9 része.

Statisztika:

207 dolgozat érkezett.
6 pontot kapott:	88 versenyző.
5 pontot kapott:	47 versenyző.
4 pontot kapott:	23 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	13 versenyző.
0 pontot kapott:	21 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2011. októberi matematika feladatai