 |
A K. 307. feladat (2011. november) |
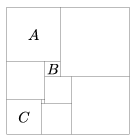
K. 307. Az ábrán látható téglalapot négyzetekre osztottuk fel hézagmentesen. Az A négyzet területe 196 cm2, a B négyzet területe 16 cm2, a C négyzet területe 81 cm2. Mennyi az eredeti téglalap területe?
(6 pont)
A beküldési határidő 2011. december 12-én LEJÁRT.
Megoldás. Az \(\displaystyle A\) négyzet oldala \(\displaystyle 14\ cm\), a \(\displaystyle B\) négyzet oldala \(\displaystyle 4\ cm\), a \(\displaystyle C\) négyzet oldala \(\displaystyle 9\ cm\). A \(\displaystyle D\) négyzet oldala \(\displaystyle A\) és \(\displaystyle B\) oldalának összege, azaz \(\displaystyle 18\ cm\), tehát a téglalap egyik oldala \(\displaystyle 14+18=32\ cm\) hosszúságú. Az \(\displaystyle E\) négyzet oldala \(\displaystyle A\) és \(\displaystyle B\) oldalának különbsége, azaz \(\displaystyle 10\ cm\), tehát a téglalap másik oldalának hossza \(\displaystyle 14+10+9=33\ cm\). A téglalap területe tehát \(\displaystyle 1056\ cm^2\).
Statisztika:
298 dolgozat érkezett. 6 pontot kapott: 210 versenyző. 5 pontot kapott: 27 versenyző. 4 pontot kapott: 30 versenyző. 3 pontot kapott: 21 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2011. novemberi matematika feladatai