 |
A K. 314. feladat (2011. december) |
K. 314. Az ábrán az AQ, BR, CP, PM, QK és RL szakaszok felezőpontjai rendre P, Q, R, K, L és M.
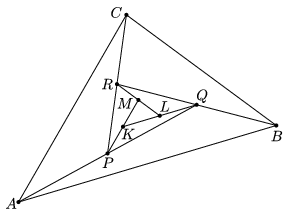
Mekkora a KLM háromszög területe, ha az ABC háromszög területe 441 cm2?
(6 pont)
A beküldési határidő 2012. január 10-én LEJÁRT.
Megoldás. Induljunk ki az \(\displaystyle PQR\) és \(\displaystyle KLM\) háromszögekből. A \(\displaystyle KLM\) és \(\displaystyle KRM\) háromszögek területe megegyezik, mert alapjuk (\(\displaystyle LM\) és \(\displaystyle RM\)) egyforma és ezekhez tartozó magasságuk is megegyezik. A \(\displaystyle KMR\) és \(\displaystyle KPR\) háromszögek területe is ugyanezen okok miatt egyenlő (\(\displaystyle KM=KP\) és ezekhez tartozó magasságuk közös). Hasonlóan, a háromszögeket kettesével tekintve (megrajzolva az \(\displaystyle RK\), a \(\displaystyle QM\) és a \(\displaystyle PL\) szakaszokat), belátható, hogy az ábrán így található 7 háromszög területe egyenlő; így a \(\displaystyle PQR\) háromszög területe a \(\displaystyle KLM\) háromszög területének hétszerese. Ugyanez a kapcsolat az \(\displaystyle ABC\) és a \(\displaystyle PQR\) háromszögek területe között is. Vagyis \(\displaystyle KLM\) területének \(\displaystyle 49\)-szerese az \(\displaystyle ABC\) területe. Tehát a kérdéses terület: \(\displaystyle 441 : 49 = 9 ~\text{\rm cm}^2\).
Statisztika:
133 dolgozat érkezett. 6 pontot kapott: 86 versenyző. 5 pontot kapott: 12 versenyző. 4 pontot kapott: 10 versenyző. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 13 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2011. decemberi matematika feladatai