A K. 330. feladat (2012. február)

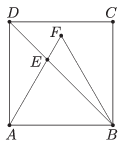
K. 330. Az ABCD négyzetbe az ábrán látható módon berajzoltuk az ABF szabályos háromszöget. Az AE hossza 2 egységnyi. Mennyi az ABCD négyzet területe?

(6 pont)

A beküldési határidő 2012. március 12-én LEJÁRT.

Megoldás. Rajzoljuk be az ábrába azt a téglalapot, melynek átlója \(\displaystyle AE\), oldalai pedig a négyzet oldalaival párhuzamosak: \(\displaystyle AXEY\), ahol \(\displaystyle X\) a négyzet \(\displaystyle AB\) oldalán van. Ekkor egyrészt az \(\displaystyle EXB\) egy egyenlő szárú, derékszögű háromszög, így \(\displaystyle EX=XB\). Másrészt az \(\displaystyle AXE\) háromszög "félszabályos", azaz egy szabályos háromszög fele, így oldalainak hossza \(\displaystyle AE=2\), \(\displaystyle AX=1\) és \(\displaystyle XE= \sqrt 3\). Ennek megfelelően a négyzet oldalának hossza \(\displaystyle AB=AX+XB=1+\sqrt 3\), azaz a területe \(\displaystyle (1+\sqrt 3)^2=4+2\sqrt 3\approx 7,46\).

Statisztika:

139 dolgozat érkezett.
6 pontot kapott:	54 versenyző.
5 pontot kapott:	31 versenyző.
4 pontot kapott:	28 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2012. februári matematika feladatai