A K. 335. feladat (2012. március)

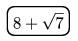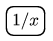K. 335. Egy különleges számológépen csak négy gomb van: (nyolc plusz gyök hét), (összeadás), (reciprok) és (egyenlő).

A számológép mindig pontos értékkel számol, és az éppen aktuális értéket a dupla lenyomásakor konstansként tárolni is tudja, azaz ezután az nyomásakor ezzel az értékkel növeli a számot akárhányszor (pl. 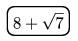        lenyomása után ezt látjuk: ). Bizonyítsuk be, hogy a

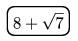
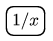
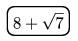
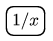
...  (56-szor)

...  (15-ször)

műveletsor eredménye 1.

(6 pont)

A beküldési határidő 2012. április 10-én LEJÁRT.

Megoldás. A feladat példája szerint a \(\displaystyle 8+\sqrt 7\) reciprokát összeadtuk egymás után 57-szer \(\displaystyle \left( \frac{57}{8+\sqrt 7}\right)= \frac{57}{8+\sqrt 7}\cdot \frac{8-\sqrt 7}{8-\sqrt 7}=\frac{57(8-\sqrt 7)}{64-7}=8-\sqrt 7)\), majd ehhez hozzáadtuk a \(\displaystyle 8+\sqrt 7\)-et (a részeredmény: 16). Ennek reciprokát véve (1/16) a reciprokot egymás után 16-szor összedatuk. A végeredmény tehát \(\displaystyle 16\cdot \frac 1{16}=1\).

Statisztika:

106 dolgozat érkezett.
6 pontot kapott:	54 versenyző.
5 pontot kapott:	9 versenyző.
4 pontot kapott:	29 versenyző.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2012. márciusi matematika feladatai