 |
A K. 342. feladat (2012. szeptember) |
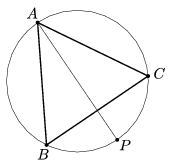
K. 342. Az ábrán látható ABC háromszög szabályos, AP az A-nál levő belső szög felezője. Bizonyítsuk be, hogy AP=BP+PC.
(6 pont)
A beküldési határidő 2012. október 10-én LEJÁRT.
Megoldás. Mivel a háromszög egyenlő szárú, ezért BP=PC. Így elég igazolni, hogy BP=AP/2. AP a kör átmérője, így Thalesz tétele miatt az ABP szög derékszög. Ekkor az ABP háromszög 60-30-90 fokos derékszögű háromszög, melyben BP a rövidebbik befogó, így egyenlő az átfogó felével. Ez éppen a bizonyítandó állítást jelenti.
Statisztika:
214 dolgozat érkezett. 6 pontot kapott: 75 versenyző. 5 pontot kapott: 56 versenyző. 4 pontot kapott: 36 versenyző. 3 pontot kapott: 13 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 10 versenyző. Nem versenyszerű: 5 dolgozat.
A KöMaL 2012. szeptemberi matematika feladatai
