 |
A K. 372. feladat (2013. február) |
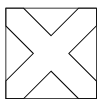
K. 372. Egy 10 cm oldalhosszúságú négyzetbe az átlókkal párhuzamos egyenesekkel rajzoltunk egy keresztet az ábrának megfelelően. A kereszt határait alkotó, a négyzeten belül haladó vonalak a csúcsoktól azonos távolságra metszik a négyzet oldalait. Mekkora a kereszt egy szárát meghatározó párhuzamos egyenesek távolsága, ha a kereszt területe 64 cm2?
(6 pont)
A beküldési határidő 2013. március 11-én LEJÁRT.
Megoldás. A négyzet területe 100 \(\displaystyle \rm{cm}^2\). A négyzetnek a kereszten kívüli része négy darab derékszögű háromszög, melyek (elforgatás nélkül) egy négyzetté tolhatók össze. Ennek területe 100 – 64 = 36 \(\displaystyle \rm{cm}^2\), így oldalának hossza 6 cm. A nagy négyzet oldalából 4 cm marad a csúcsoktól vett távolságokra, tehát a kereszt szárát alkotó párhuzamosok a csúcsoktól 2 cm-re érnek ki a négyzet oldalaira. A keresett távolság így egy 2 cm befogójú, egyenlő szárú derékszögű háromszög átfogója, azaz \(\displaystyle 2\sqrt2\) cm.
Statisztika:
128 dolgozat érkezett. 6 pontot kapott: 93 versenyző. 5 pontot kapott: 13 versenyző. 4 pontot kapott: 3 versenyző. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2013. februári matematika feladatai