A K. 422. feladat (2014. szeptember)

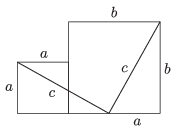
K. 422. Egy \(\displaystyle a\) és egy \(\displaystyle b\) oldalú négyzetet egymáshoz illesztünk, majd két \(\displaystyle c\) hosszúságú szakasszal az ábrán látható módon szétvágjuk a két négyzetet összesen 5 darab síkidomra. Mutassuk meg, hogy a keletkező 5 darabból hézag- és átfedésmentesen összeállítható egy \(\displaystyle c\) oldalú négyzet.

(6 pont)

A beküldési határidő 2014. október 10-én LEJÁRT.

Megoldás. Az ábrán jelöljük meg 1, 2, 3, 4 és 5 számokkal a keletkező darabokat. Az 1-es és 4-es darab együtt, valamint az 5-ös egy \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) oldalú derékszögű háromszög. Emiatt az ábrán jelzett \(\displaystyle \alpha\) és \(\displaystyle \beta\) szögek összege \(\displaystyle 90^{\circ}\). A 2-es és 3-as darabot a helyükön hagyjuk. Az 5-öst balra fel csúsztatjuk, ez pont illeszkedik a 2-es tetejére, mert így az \(\displaystyle a\) hosszúságú oldalaik találkoznak. Az 1-est és 4-est együtt jobbra fel csúsztatjuk, akkor ezek pont illeszkednek a 3-as darab \(\displaystyle b\) hosszúságú felső oldalára. Tekintve, hogy a 3-as darabnak a 2-es fölé kilógó része és az 1-es darab \(\displaystyle a\) oldala együtt éppen \(\displaystyle b\) hosszú, azért az 5-ös és az 1-es felső csúcsa pont találkozik egymással. A létrejövő alakzat négyzet, mert minden oldala c hosszúságú, és szögei derékszögek az ábráról leolvasható módon.

Statisztika:

130 dolgozat érkezett.
6 pontot kapott:	Fekete Balázs Attila, Kós Anna, Kubovics Márton, Perényi Gellért, Sántha 001 Balázs, Sisák László Sándor, Szarka Álmos, Szilágyi Botond, Valkó Bence.
5 pontot kapott:	Bácskai Zsombor, Cu Le Dieu Huong, Encz Koppány, Harsányi Benedek, János Zsuzsa Anna, Sepp Márton.
4 pontot kapott:	18 versenyző.
3 pontot kapott:	17 versenyző.
2 pontot kapott:	16 versenyző.
1 pontot kapott:	46 versenyző.
0 pontot kapott:	14 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2014. szeptemberi matematika feladatai