A K. 481. feladat (2015. december)

K. 481. Mennyi a számok összege a \(\displaystyle 20\times 20\)-as szorzótáblában? (Az ábrán az \(\displaystyle 5\times 5\)-ös szorzótáblát látjuk.)

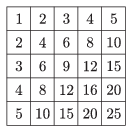
(6 pont)

A beküldési határidő 2016. január 11-én LEJÁRT.

Megoldás. A \(\displaystyle 20\times2\)0-as szorzótábla első sorában a számok összege \(\displaystyle 1 + 2 + 3 + \ldots + 20 = 210\). A másodikban ennek a kétszerese, a harmadikban a háromszorosa, a huszadikban a 20-szorosa. Tehát a táblázatban levő számok összege \(\displaystyle 210 \cdot (1 + 2 + 3 + \ldots + 20) = 210 \cdot 210 = 44\,100\).

Statisztika:

146 dolgozat érkezett.
6 pontot kapott:	120 versenyző.
5 pontot kapott:	14 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2015. decemberi matematika feladatai