A K. 489. feladat (2016. január)

K. 489. Péter beírta az első 2015 pozitív egész számot egy \(\displaystyle 100\times 100\)-as táblázatba az ábrának megfelelően. (Az ábrán látható kitöltés még nem teljes.) Melyik számot írta a 2. sorban utolsóként?

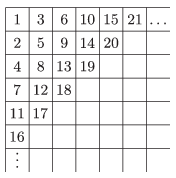
(6 pont)

A beküldési határidő 2016. február 10-én LEJÁRT.

Megoldás. A második sorban a szomszédos számok különbsége rendre 1-gyel nő, mert az átlók hossza rendre 1-gyel nő:

\(\displaystyle 2 + (2 + 3) + ( 2 + 3 + 4) + (2 +3 + 4 +5) + {\dots} + (2 + 3 + 4 + 5 + {\dots} + x).\)

\(\displaystyle 2 + 3 + 4 + 5 + {\dots} + {x} {\leq} 2015\), így \(\displaystyle 1 + 2 + 3 + 4 + 5 + {\dots} + {x} \ = \frac{(1 + x) \cdot{x}}{ 2} {\leq} 2016\), ahonnan \(\displaystyle (1 + {x}) \cdot {x} \ {\leq} 4032\), vagyis \(\displaystyle {x}^2 + {x} {\leq} 4032\).

Becsüljük meg \(\displaystyle {x}\) értékét! \(\displaystyle 60<x<70\), majd pontosítva \(\displaystyle x = 63\). Így a második sor utolsó tagja \(\displaystyle \frac{63\cdot 64} 2-1=2015\).

Statisztika:

102 dolgozat érkezett.
6 pontot kapott:	Bartha Ákos, Bertók Zsanett, Csóka Zoárd, Dékány Barnabás, Dobák Dániel, Fabó Bence Richárd, Fekete Barnabás, Gálffy Veronika, Gilicze Márton, Hoffmann Balázs, Jankovits András, Kávási Tamás, Keltai Dóra, Kertész Ferenc, Kluèka Vivien, Kovács 161 Márton Soma, Kovács 576 Kristóf, Marshall Tamás, Marton Laura, Mester Gyöngyvér, Mészáros 916 Márton, Miskolczi Abigél, Mónos Péter, Nagy Csaba Jenő, Nemes Balázs Boldizsár, Nyitrai Boglárka, Pálvölgyi Szilveszter, Pinke Jakab Zoltán, Pipis Panna, Polonyi Domonkos, Ruzsa Kata, Sal Dávid, Szöllősi Brigitta, Varga 294 Ákos, Zsótér Laura.
5 pontot kapott:	Bálint Szilárd, Csáfordi József, Kiss 468 Péter, Nagy Gábor János, Piller Ádám.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	12 versenyző.
Nem versenyszerű:	10 dolgozat.

A KöMaL 2016. januári matematika feladatai