A K. 498. feladat (2016. február)

K. 498. Egy körvonalat felosztottunk 12 egyenlő részre, majd az osztópontokat összekötöttük az ábrának megfelelően. Határozzuk meg az így keletkezett rombuszok területeinek arányát.

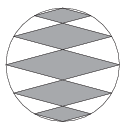
(6 pont)

A beküldési határidő 2016. március 10-én LEJÁRT.

Megoldás. A megfelelő átlók hosszának felét tudjuk így meghatározni, melyek: \(\displaystyle OD = r\), \(\displaystyle XC\) és \(\displaystyle YB\). Az \(\displaystyle OCX\) derékszögű háromszögben az \(\displaystyle XOC\) szög \(\displaystyle 60^{\circ}\)-os, hiszen az \(\displaystyle AC\) körív a körvonal hatoda. Így \(\displaystyle XO = OC/2 = r/2\). A Pitagorasz-tétel alapján \(\displaystyle XC^2 = OC^2 – XO^2 = r^2 – (r/2)^2\), ahonnan \(\displaystyle XC = \frac{\sqrt3r}{2}\). Az \(\displaystyle OBY\) háromszög szintén \(\displaystyle 30^{\circ}-60^{\circ}-90^{\circ}\)-os háromszög, mert az \(\displaystyle AB\) ív a körív \(\displaystyle 12\)-ed része. Így \(\displaystyle YB = OB/2 = r/2\). A teljes átlók hossza tehát: \(\displaystyle 2r\), \(\displaystyle \sqrt3\) és \(\displaystyle r\), a területek aránya pedig ezek négyzeteinek aránya: \(\displaystyle 1: 3: 4 : 3: 1\).

Statisztika:

46 dolgozat érkezett.
6 pontot kapott:	Barta Ákos, Csáfordi József, Csóka Zoárd, Debreczeni Tibor, Dékány Barnabás, Dobák Dániel, Gilicze Márton, Gortka Bence, Kluèka Vivien, Marshall Tamás, Mester Gyöngyvér, Mészáros 916 Márton, Nagy Csaba Jenő, Nyitrai Boglárka, Pálvölgyi Szilveszter, Pinke Jakab Zoltán, Rubovszky Cecília , Sal Dávid, Simon Dóra, Varga 294 Ákos.
5 pontot kapott:	Bertók Zsanett, Fekete Barnabás, Földvári Ádám, Gálffy Veronika, Gárdonyi Csilla Dóra, Keltai Dóra, Kertész Ferenc, Kovács 576 Kristóf, Kovács Levente András, Póta Balázs.
4 pontot kapott:	2 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	7 versenyző.

A KöMaL 2016. februári matematika feladatai