A K. 518. feladat (2016. november)

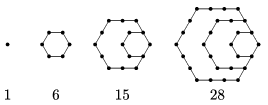
K. 518. Hatszögszámnak nevezzük az ábrasor számait és az ábrasor folytatásában megjelenő további számokat. Bizonyítás nélkül adjunk képletet az $\displaystyle n$-edik hatszögszámra, majd ez alapján mutassuk meg, hogy a 2016 hatszögszám.

(6 pont)

A beküldési határidő 2016. december 12-én LEJÁRT.

Megoldás. „Emeletenként” nézve: $\displaystyle 1 = 1 \cdot 1$, $\displaystyle 6 = 3 \cdot 2$, $\displaystyle 15 = 5 \cdot 3$, $\displaystyle 28 = 7 \cdot 4$, az ötödik hatszögszám $\displaystyle 9 \cdot 5 = 45$, a hatodik pedig $\displaystyle 11 \cdot 6 = 66$ és így tovább. Az n. hatszögszám $\displaystyle (2n – 1) \cdot n$. Mivel $\displaystyle 2016 = 63 \cdot 32$, így a 2016 a 32. hatszögszám.

Statisztika:

101 dolgozat érkezett.
6 pontot kapott:	84 versenyző.
4 pontot kapott:	6 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2016. novemberi matematika feladatai