A K. 526. feladat (2016. december)

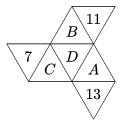
K. 526. Az ábrán minden betű és szám különböző prímszámok, valamint bármely négy, ,,egy egyenesben'' fekvő háromszögben lévő szám összege egyenlő. Mekkora ennek az összegnek a legkisebb lehetséges értéke?

(6 pont)

A beküldési határidő 2017. január 10-én LEJÁRT.

Megoldás. $\displaystyle B + D + A + 13 = A + D + C +7$, ahonnan $\displaystyle B + 6 = C$.

$\displaystyle A + D + C + 7 = C + D + B +11$, ahonnan $\displaystyle A = B + 4$.

Vagyis $\displaystyle C = A + 2$ és $\displaystyle B$, $\displaystyle B+4$, $\displaystyle B+6$ egyaránt prímszámok.

A prímszámok: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, …

Mivel a 7, 11, 13 már szerepel a számok között, így a legkisebb lehetséges érték $\displaystyle A = 41$, $\displaystyle B = 37$, $\displaystyle C = 43$, ekkor $\displaystyle D = 2$. Az összeg legkisebb értéke 93.

(Ellenőrzés: $\displaystyle 93 = 41 + 2 + 43 + 7 = 43 + 2 + 37 + 11 = 37 + 2 + 41 + 13)$.

Statisztika:

99 dolgozat érkezett.
6 pontot kapott:	52 versenyző.
5 pontot kapott:	16 versenyző.
4 pontot kapott:	22 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	5 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2016. decemberi matematika feladatai