 |
A K. 535. feladat (2017. február) |
K. 535. El lehet-e helyezni az 1, 2, 3, 4, 5, 6, 7, 8, 9 és 10 számokat az ábrán látható csillagötszögben úgy, hogy minden négy számot tartalmazó egyenes mentén az összeg ugyanannyi legyen?
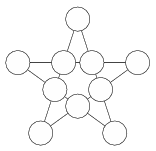
(6 pont)
A beküldési határidő 2017. március 10-én LEJÁRT.
Megoldás. Minden szám pontosan két összegben szerepel. \(\displaystyle 2 \cdot (1 +2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) = 110\), így minden egyenes mentén 110 : 5 = 22 kell legyen a számok összege.
Próbáljuk megkeresni, hogy az 1-est tartalmazó két egyenesen mely számok szerepelhetnek még. Hét számnégyes alkotható az 1-10-ig terjedő számokból úgy, hogy a bennük szereplő négy szám összege 22 legyen, és az 1-est tartalmazzák: 1,2 9,10; 1,3,8,10; 1,4,7,10; 1,4,8,9; 1,5,6,10; 1,5,7,9; 1,6,7,8. Annak a két egyenesnek, amelyeknek az 1-es közös eleme, más közös eleme nem lehet. Így a fenti számnégyesekből három olyan pár alkotható, melyek az 1-est tartalmazó két egyenesen szereplő számok lehetnek:
| egyik egyenesen szereplő számok | másik egyenesen szereplő számok | a hiányzó számok, melyek másol állnak | |
| I. eset | 1,2,9,10 | 1,6,7,8 | 3,4,5 |
| II. eset | 1,3,8,10 | 1,5,7,9 | 2,4,6 |
| III. eset | 1,4,8,9 | 1,5,6,10 | 2,3,7 |
I. eset. A 2, 9 és a 10-es számhoz is kell egy-egy számot választani a 6,7 és 8 közül úgy, hogy a 3,4,5 közül valamelyik kettővel az összeg 22 legyen. Nézzük először a 10-et. 22-10-6=6, de 3+4=7 már több a 6-nál. Ha nem a 6-ot, hanem a 7-et vagy a 8-at választjuk, akkor is nagyobb lesz a 7 a szükséges számnál.
II. eset. Az első esethez hasonlóan a 10-et nézzük, hozzá kell az 5, 7 és 9 számok közül választani egyet úgy, hogy a 2,4,6 közül valamelyik kettővel az összeg 22 legyen. Mivel 22-10-5=7, de a 2,4,6-ból képezhető összegek mind párosak, ez nem lehetséges. Az 5 helyett a 7 és a 9 választása esetén is ugyanez a helyzet.
III. eset. Itt a második oszlopban szerepel a 10, amihez a 4,8,vagy 9 közül egyet, illetve a 2,3,7 közül kell kettőt kiválasztani. Ez utóbbi esetén a lehetséges összegek: 2+3=5, 2+7=9 és 3+7=10. Mivel 22-10-4=8, 22-10-8=4 és 22-10-9=3, ezért itt sem jutunk célhoz.
Tehát nem lehet így elrendezni a számokat.
Csikós Patrik (Budapest, XIV. Kerületi Szent István Gimnázium) megoldása alapján
Statisztika:
53 dolgozat érkezett. 6 pontot kapott: Acs Imre, Bérczi Péter, Gém Viktória, Juhász 315 Dorka, Kis 194 Károly, Kovács Fruzsina Dóra, Markó Gábor, Rátki Luca, Rusvai Miklós, Székelyhidi Klára, Szemerédi Előd, Vincze Lilla. 5 pontot kapott: Csikós Patrik, Sándor 111 Réka. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 22 versenyző. 1 pontot kapott: 14 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2017. februári matematika feladatai

