A K. 544. feladat (2017. március)

K. 544. Háromszögszámoknak nevezzük azokat a számokat, amelyek előállnak az első valahány egymást követő természetes szám összegeként (\(\displaystyle 1, 3, 6, 10, \ldots\)). Hatszögszámnak nevezzük az alábbi ábrasor számait és az ábrasor folytatásában megjelenő további számokat. Adjuk meg az összes olyan hatszögszámot, amely háromszögszám is.

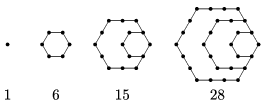
(6 pont)

A beküldési határidő 2017. április 10-én LEJÁRT.

Megoldás. ,,Emeletenként" nézve: \(\displaystyle 1 = 1 \cdot 1\), \(\displaystyle 6 = 2 \cdot 3\), \(\displaystyle 15 = 3 \cdot 5\), \(\displaystyle 28 = 4 \cdot 7\) és így tovább. Az \(\displaystyle n\). hatszögszám \(\displaystyle n(2n – 1)\). A \(\displaystyle k\). háromszögszám \(\displaystyle \frac{k(k+1)}{2}\).

Megoldandó a \(\displaystyle \frac{k(k+1)}{2}=n(2n-1)\) diofantikus egyenlet a pozitív számok halmazán. 2-vel beszorozva: \(\displaystyle k(k+1)=2n(2n-1)\), \(\displaystyle k^2+k=4n^2-2n\), átrendezve és szorzattá bontva: \(\displaystyle 2n+k=4n^2-k^2=(2n+k)(2n-k)\), ahonnan a pozitív \(\displaystyle (2n+k)\)-val elosztva: \(\displaystyle 1 = 2n – k\), vagyis \(\displaystyle k=2n-1\).

Tehát az \(\displaystyle n\)-dik hatszögszám éppen a \(\displaystyle (2n – 1)\)-dik háromszögszám, azaz minden hatszögszám háromszögszám is. (Illetve minden páratlanadik háromszögszám egyúttal hatszögszám is.)

Statisztika:

54 dolgozat érkezett.
6 pontot kapott:	Acs Imre, Balogh Bence, Bérczi Péter, Cseh Dániel, Espán Márton, Gém Viktória, Gyuricza Gergő, Hegedűs Eszter, Juhász 315 Dorka, Kincses Benedek, Kis 194 Károly, Kocsor Dániel, Kozák 023 Áron, Lakatos Zselyke, Lezsák Domonkos, Markó Gábor, Mátravölgyi Bence, Német Franciska, Op Den Kelder Júlia, Paróczai Anett, Pásti Bence, Purgel Dóra, Rátki Luca, Rittberger András, Rusvai Miklós, Sepsi Csombor Márton, Szente Péter, Vass Erik Márk, Vincze Lilla.
5 pontot kapott:	Csikós Patrik, Dombai Zétény, Fenyvesi Tamás, Nagy 345 Bálint, Pálfi Bálint, Szemerédi Előd.
4 pontot kapott:	10 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	1 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2017. márciusi matematika feladatai