A K. 545. feladat (2017. március)

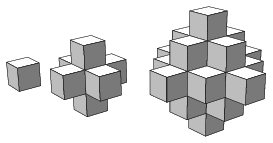
K. 545. Balázs kis kockákból elkészítette az ábrán látható három testet. Hány kockából állna a 10. test, ha ugyanígy építkezne tovább?

(6 pont)

A beküldési határidő 2017. április 10-én LEJÁRT.

Megoldás. Számoljunk rétegenként: a tizedik építményben 1-es, 2-es, 3-as, ..., 10-es rétegek vannak, bennük rendre 1, \(\displaystyle 4 + 1 = 5\) és \(\displaystyle 9 + 4 = 13\),..., \(\displaystyle 10^2 + 9^2\) kis kockával, ugyanis az egyes rétegekben sakktáblaszerű színezést alkalmazva kiderül, hogy az \(\displaystyle n\). szinten \(\displaystyle n^2+(n-1)^2\) darab kocka van.

A tizedik testben összesen:

\(\displaystyle 1^2+(2^2+1^2)+(3^2+2^2)+...+(9^2+8^2)+(10^2+9^2)+(9^2+8^2)+...+(3^2+2^2)+(2^2+1^2)+1^2=\)

\(\displaystyle =4\cdot(1^2+2^2+3^2+\dots+8^2)+3\cdot9^2+10^2\)

kockából áll.

Ami számológéppel, vagy az első \(\displaystyle n\) pozitív négyzetszám összegére vonatkozó képlettel számolva:

\(\displaystyle 4\cdot\frac{8\cdot9\cdot17}{6}+3\cdot9^2+10^2=1159.\)

Tehát a 10. test 1159 kockából áll.

Statisztika:

61 dolgozat érkezett.
6 pontot kapott:	51 versenyző.
4 pontot kapott:	2 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2017. márciusi matematika feladatai