A K. 557. feladat (2017. október)

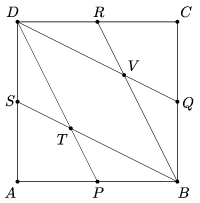
K. 557. Egy $\displaystyle ABCD$ négyzet $\displaystyle P$, $\displaystyle Q$, $\displaystyle R$ és $\displaystyle S$ oldalfelező pontjait összekötöttük a négyzet csúcsaival az ábrán látható módon. Bizonyítsuk be, hogy $\displaystyle AT = TV$.

(6 pont)

A beküldési határidő 2017. november 10-én LEJÁRT.

Megoldás. Szimmetria miatt $\displaystyle T$ és $\displaystyle V$ az $\displaystyle AC$ átló egyenesén vannak, $\displaystyle AK=KC$ és $\displaystyle TK=KV$.

Az $\displaystyle ABD$ háromszögnek $\displaystyle T$ a súlypontja, mert $\displaystyle BS$ és $\displaystyle DP$ súlyvonalak. A $\displaystyle DBC$ háromszögnek $\displaystyle V$ a súlypontja, mert $\displaystyle BR$ és $\displaystyle DQ$ súlyvonalak. A háromszög súlypontja a csúcstól távolabbi harmadoló pont a súlyvonalon. Ezért $\displaystyle AT = 2TK=TK+ KV =TV$.

Statisztika:

122 dolgozat érkezett.
6 pontot kapott:	53 versenyző.
5 pontot kapott:	22 versenyző.
4 pontot kapott:	13 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	12 dolgozat.

A KöMaL 2017. októberi matematika feladatai