A K. 597. feladat (2018. október)

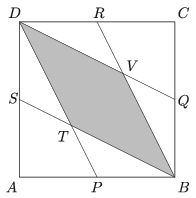
K. 597. Az \(\displaystyle ABCD\) négyzet \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) és \(\displaystyle S\) oldalfelező pontját az ábrán látható módon összekötöttük a négyzet csúcsaival. Határozzuk meg a \(\displaystyle BVDT\) négyszög és az \(\displaystyle ABCD\) négyzet területének arányát.

(6 pont)

A beküldési határidő 2018. november 12-én LEJÁRT.

Megoldás. A \(\displaystyle DBC\triangle\)-nek \(\displaystyle V\) a súlypontja, így a \(\displaystyle DBV\triangle\) területe a \(\displaystyle DBC\triangle\) területének a harmada, hiszen a \(\displaystyle BD\) oldaluk közös és a \(\displaystyle V\) pont (a csúcstól távolabbi harmadoló pont a súlyvonalon, így a) távolsága \(\displaystyle DB\)-től harmadannyi, mint a \(\displaystyle C\) pont távolsága, vagyis a \(\displaystyle DBV\triangle\) \(\displaystyle DB\) oldalhoz tartozó magassága harmada a \(\displaystyle DBC\) háromszög \(\displaystyle DB\) oldalhoz tartozó magasságának. Hasonló igaz a \(\displaystyle DBT\triangle\) területére, így a \(\displaystyle BVDT\) négyszög területe harmada az \(\displaystyle ABCD\) négyzet területének.

Statisztika:

169 dolgozat érkezett.
6 pontot kapott:	51 versenyző.
5 pontot kapott:	14 versenyző.
4 pontot kapott:	14 versenyző.
3 pontot kapott:	21 versenyző.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	13 versenyző.
0 pontot kapott:	14 versenyző.
Nem versenyszerű:	5 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	22 dolgozat.

A KöMaL 2018. októberi matematika feladatai