 |
A K. 598. feladat (2018. október) |
K. 598. A digitális órákon a számjegyek rövid pálcika-lámpákból állnak, ahogy az ábrán látható:
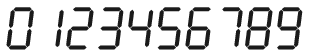
Az órák fogyasztását az határozza meg, hogy mennyi kis pálcika-lámpát kell ki-be kapcsolni, ahogy változik az idő. Például 3-ról 4-re váltásnál két pálcika-lámpát kell ki- és egyet bekapcsolni, ami három kapcsolást jelent. Egy teljes \(\displaystyle 0, 1, 2, \ldots, 9, 0\) ciklus alatt ez összesen harminc kapcsolás. Ha ugyanezeket a digitális jeleket más sorrendben használnánk a 0-tól 9-ig terjedő számok megjelenítésére, akkor kevesebb kapcsolás is elég lenne. Keressük meg a kapcsolások egy teljes ciklusra vonatkozó számának minimumát, és adjunk meg hozzá egy megfelelő számjegy-sorrendet.
Javasolta: Ruttkai Zsófia (Hollandia)
(6 pont)
A beküldési határidő 2018. november 12-én LEJÁRT.
Megoldás. Két szám távolságán most a köztük lévő szükséges kapcsolások számát értjük. Minden számhoz megkeressük a hozzá legkisebb (1 vagy 2) távolságra lévő számokat. A táblázat első sorában és oszlopában a számok, a többi helyen ezek távolsága van (csak az 1 és 2 távolságok).
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 2 | 1 | 2 | |||||||
| 1 | 2 | 1 | ||||||||
| 2 | 2 | 2 | ||||||||
| 3 | 2 | 2 | 2 | 2 | 1 | |||||
| 4 | 2 | 2 | ||||||||
| 5 | 2 | 1 | 1 | |||||||
| 6 | 2 | 1 | 1 | 2 | ||||||
| 7 | 1 | 2 | ||||||||
| 8 | 1 | 2 | 2 | 1 | 1 | |||||
| 9 | 2 | 1 | 2 | 1 | 2 | 1 |
Mivel teljes ciklust kell leírnunk, minden szám előtt és után is kell állnia számnak (az elején és a végén ugyanaz a szám áll). Minden számhoz tartozik két legkisebb távolság, a sorában szereplő két legkisebb szám, ez a 0-nál 1 és 2, az 1-nél szintén 1 és 2, a 2-nél 2 és 2 stb. Ha ezeket összeadjuk, megkapjuk, hogy az adott szám minimum hány kapcsolással kivitelezhető a ciklusban. Ezek összege \(\displaystyle 3+3+4+3+4+2+2+3+2+2=28\). Ezt elosztva kettővel (mert minden távolságot kétszer számoltunk) megkapjuk azt az elméleti minimumot, aminél kevesebb kapcsolással biztosan nem vihető végbe a teljes ciklus. Ez az összeg \(\displaystyle \frac{28}{2}=14\). Azonban a megvalósítható minimum ennél nagyobb, a következők miatt. A 2-es előtt és után a fenti legkisebb távolságok miatt a 8-as és a 3-as áll (a sorrend mindegy), de a 8-asnál keletkező legkisebb távolságok összege, a 2 egység úgy jönne ki, ha a 8-as szomszédai a 6, a 9 vagy a 0 lennének, mert ezek vannak 1 távolságra tőle. Emiatt a 8-asnál számolt legkisebb távolságok összege 1-gyel nő. Hasonló okok miatt a 4-es előtt vagy után 9-esnek kell állnia, aminek a 2 egységnyi eredeti minimumát ez szintén növeli 1-gyel. A 9-es másik oldalán az elméleti minimum szerint a 3-nak és az 5-nek egyszerre kellene lennie, ez nem lehet, ezért vagy a hármasnál vagy az ötösnél ez újabb emelést jelent 1-gyel. Hasonló okok miatt a 8-as egyik oldalán mindenképp a 2-esnek kell állnia, ami miatt a másik oldalon az elméleti minimum szerint a 0-nak és a 6-nak egyszerre kellene lennie. Ez szintén növeli 1-gyel az elméleti minimumot. Az előbbiek alól kivételt csak az az eset képezne, ha a 2-esnél a 8 helyett egy másik szomszédot választanánk, de akkor ez már önmagában legalább 2-vel növeli a vizsgált összeget, hasonlóan a 4-esnek választhatunk a 9-es helyett másik szomszédot, de ez is tovább növelné a kapcsolások számát. Így az elméleti 28-as minimum (a 2-vel való osztás előtt) összesen legalább 4-gyel nőtt, azaz a valódi minimum \(\displaystyle \frac{32}{2}=16\).
Több olyan ciklus is elképzelhető, aminek a kapcsolási összege 16, egy példa: 14956082371.
Hoffmann Szabolcs (Egri Szilágyi E. Gimn., 9. évf.)
Statisztika:
170 dolgozat érkezett. 6 pontot kapott: Egyházi Hanna, Hoffmann Szabolcs, Kalocsai Zoltán, Miklóssy Katinka, Toronyi András. 5 pontot kapott: Ferjancsik Zaránd, Sebestyén Pál Botond, Szirmai Dénes. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 11 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 27 versenyző. 0 pontot kapott: 96 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 19 dolgozat.
A KöMaL 2018. októberi matematika feladatai

