 |
A K. 60. feladat (2005. november) |
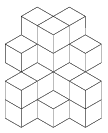
K. 60. Az ábrán látható építményt úgy kaptuk, hogy egyforma méretű kockákat ragasztottunk össze. Két kocka összeragasztásához szükséges, hogy két lapjuk valamely mértékben átfedje egymást (tehát ha csak élben találkoznak, az nem elég). Határozzuk meg, hogy legalább hány kockából készíthető el az építmény.
(6 pont)
A beküldési határidő 2005. december 12-én LEJÁRT.
Megoldás: Az ábrán láthatunk 13 kockát, és nyilván vannak nem látható kockák, melyek egyben tartják a többit.

Az 1, 2, 3 jelű kockák rögzítéséhez darabonként egy nem látható kocka szükséges, ugyanis ezek távolsága akkora, hogy egy kocka nem tud közülük kettőhöz csatlakozni ragasztási felülettel. Össze kell még ragasztani a 4, 5 6 jelű kockákat is, ehhez kell egy kocka. Ez a kocka nem lehet az, amelyik pl. az 1-es kockát rögzíti, mert az 1, 4, 5 jelű kockáknak elhelyezkedésük miatt nem lehet egy (nem látható) kockával közös ragasztási felületük. Tehát legalább négy nem látható kocka szükséges a rögzítéshez. Ez elég is: a 4, 5, 6 jelű kockák a természetesen mögéjük kívánkozó, hozzájuk teljes oldallal csatlakozó kockával összeragaszthatók, az 1 és 2 jelű kockákat a hozzájuk, illetve az 5 jelű kockához teljes lappal csatlakozó egy-egy kockával rögzíthetjük, a 3 jelűt pedig hozzá és a 4-eshez vagy 6-oshoz teljes lappal csatlakozó kockával tudjuk felragasztani. Az építmény tehát legalább 17 kockából áll.
Statisztika:
197 dolgozat érkezett. 6 pontot kapott: 109 versenyző. 4 pontot kapott: 7 versenyző. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 22 versenyző. 0 pontot kapott: 53 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2005. novemberi matematika feladatai

