A K. 605. feladat (2018. december)

K. 605. Kehelynek nevezünk három kiskockát, ha párosával egy-egy közös élük van (lásd az ábrát). Egységnyi élhosszúságú kiskockákból téglatesteket építettünk.

$\displaystyle a)$ Hány kehely található egy $\displaystyle 4\times4\times2$-es téglatestben?

$\displaystyle b)$ Hány kehely található egy $\displaystyle 4\times4\times3$-as téglatestben?

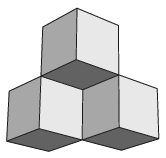
(6 pont)

A beküldési határidő 2019. január 10-én LEJÁRT.

Megoldás. Tekintsük azt a kiskockát, ami beleillik a kehelybe (mindhárom kockával lesz közös lapja), illetve azt a $\displaystyle 2\times2\times2$-es kockát, melyre a kehely kiegészíthető. Minden $\displaystyle 2\times2\times2$-es kockában 8 kehely van (a kocka minden egyes csúcsnál lévő kis kockája egy-egy ilyen kehelybe illő kis kocka).

a) A $\displaystyle 4\times4\times2$-es téglatest 9 darab $\displaystyle 2\times2\times2$-es kocka alakú részt tartalmaz (lásd az ábrát, ahol felülnézetben rajzoltuk be a $\displaystyle 4\times4\times2-$es téglatestbe a $\displaystyle 2\times2\times2$-es kocka lehetséges helyét), így $\displaystyle 9\cdot8=72$ kehely van ebben a téglatestben.

b) A $\displaystyle 4\times4\times3$-as téglatest alsó $\displaystyle 4\times4\times2$-es része 9 darab $\displaystyle 2\times2\times2$-es kockát tartalmaz, akárcsak a felső $\displaystyle 4\times4\times2$-es része, így összesen $\displaystyle 2\cdot72=144$ kehely van a téglatestben.

Statisztika:

103 dolgozat érkezett.
6 pontot kapott:	51 versenyző.
5 pontot kapott:	6 versenyző.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	11 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	5 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	13 dolgozat.

A KöMaL 2018. decemberi matematika feladatai